Einführung in das Wiggle Matching

Einführung in die Bayes ’sche Statistik.

„It's taken 250 years for the rest of us to realize just how intelligent Thomas Bayes was. “

Mike R. Lynch 2001

Textabbildung 26, Reverend Thomas Bayes, 1702-1761.

Beschreibung: http://www.bayesian.org/bayes.jpeg

Bayes'sche Methoden werden in der Statistik zunehmend populär, insbesondere für komplexe Fragestellungen wie Mustererkennung oder inverse Probleme der Datenanalyse. Diese "Renaissance" wurde ausgelöst durch die schnelle Zunahme der zur Verfügung stehenden Rechenleistung, prinzipielle Probleme der "klassischen Statistik", sowie durch eine fruchtbare Verbindung zur Statistischen Physik z. B. auf dem Gebiet der Monte-Carlo-Methoden. Die hauptsächlichen Berechnungen im Bereich der Auswertung von ¹⁴C-Daten sind Integrale, die mittels eines MCMC-Samplers möglichst viele unterschiedliche Lösungen berechnen, um ein optimales Resultat zu finden.

$Beschreibung: C:\www\www.winserion.org\docs\LVAS\QAM\14C\economist.fig.jpg$

Bayes'sche Statistik steht dabei im Gegensatz zur konventionellen Statistik der Frequentisten.

Wichtige Elemente der Bayes'schen Statistik sind die a priori und a posteriori Verteilungen auf dem Parameterraum. Die a priori Verteilung ermöglicht es dem Statistiker, zusätzliche Information in das statistische Modell einzubringen.

Die Essenz der Bayes’schen Annäherung ist es, ein mathematisches Gesetz zu formulieren, wie man sein vorhandenes Wissen im Lichte neuer Evidenz verändern sollte. Anders gesagt, es erlaubt dem Wissenschaftler neue Daten mit seinem vorhandenen Fachwissen zu kombinieren.

Ein erklärendes Beispiel dazu mag das Verhalten eines Babys sein, das den ersten Sonnenuntergang erlebt, und sich fragt, ob die Sonne wieder aufgehen wird oder nicht. Es gibt beiden Möglichkeiten gleich große „prior“ Wahrscheinlichkeiten und demonstriert das, indem es sowohl eine weiße als auch eine schwarze Kugel in einen Sack gibt. Am nächsten Tag, wenn die Sonne wieder aufgeht, gibt das Kind wieder eine weiße Kugel in den Sack. Die Wahrscheinlichkeit, dass eine zufällig aus dem Sack gegriffene Kugel eine weiße ist (und damit die Erwartungen des Kindes repräsentiert), hat sich von zu verändert. U. s. w. Graduell wird die ursprüngliche Meinung, dass die Sonne genauso wahrscheinlich nicht mehr aufgeht wie dass sie aufgeht, in eine fast vollständige Sicherheit verändert, dass sie immer aufgeht.

In einer mathematischen Formel ausgedrückt bedeutet das Bayes'sche Gesetz:

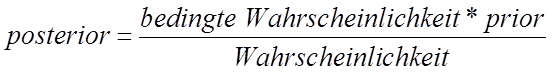
oder in mathematischen Symbolen:

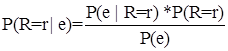
wobei die Wahrscheinlichkeit bedeutet, dass die zufällige Variable R einen Wert r bei gegebener Tatsache e hat. Der Nenner ist nur eine Normalsierungskonstante, die sicherstellt, dass das posterior einen Wert kleiner 1 ergibt. Dieser Nenner kann berechnet werden, indem alle Wahrscheinlichkeiten für alle möglichen Werte von R addiert werden.

In den folgenden Beispielen wird das archäologische Vorwissen als prior aufgefasst, ob das nun von der Kenntnis der Stratigrafie, Dendrochronologie, intuitiv oder durch andere mathematische Verfahren wie Seriation, Korrespondenzanalyse oder Analyse der N Nächsten Nachbarn stammt, um die ¹⁴C-Kalibration in der posteriori Analyse einzuschränken.

Methodik und Theorie

Dieses Kapitel wurde aus folgendem Artikel übernommen: Stadler Peter, Ruttkay Elisabeth, Doneus Michael, Friesinger Herwig, Lauermann Ernst, Kutschera Walter, Neubauer Wolfgang, Neugebauer-Maresch Christine, Trnka Gerhard, Weninger Franz, Wild Eva Maria 2006 (2005), Absolutchronologie der Mährisch-Ostösterreichischen Gruppe (MOG) der bemalten Keramik aufgrund von neuen ¹⁴C-Datierungen. Archäologie Österreichs 17/2, Festschrift Ruttkay, 53-81, die Abbildungen stammen zum großen Teil von Franz Weninger.

Liegt eine Menge von ¹⁴C-Messungen vor und will man eine Aussage über ihre Einheitlichkeit machen, so sind die wichtigsten Maßzahlen die Anzahl der Messungen, der Mittelwert und die Standardabweichung. Letztere ist eine Maßzahl der Streuung. Wird in der Statistik eine Auswertung über eine Menge von Werten benötigt, gibt die Standardabweichung ein sinnvolles Maß für die Streuung um den Mittelwert an. Sie heißt auch mittlerer Fehler. Als mathematisches Zeichen ist dabei σ üblich. Oft nennt man den mittleren Fehler auch Plus/Minus (±) und schreibt ihn direkt hinter den Mittel- bzw. Durchschnittswert.

Für jedes ¹⁴C Messergebnis werden zwei Werte angegeben:

1) Der Messwert in Jahren BP (BP heißt before present, also vor heute und ist das unkalibrierte Ergebnis der ¹⁴C-Messung)

2) Der Messfehler, auch als Sigma (σ) bezeichnet, in Jahren. Z. B. für Friebritz Grab Verfärbung 130 wurde bei der Messung VERA-1976 ein Messwert von 5888 BP mit einem σ von 38 (Jahren) angegeben.

Die 1950 entwickelte ¹⁴C-Methode ging zunächst davon aus, dass das ¹⁴C in der Erdatmosphäre durch die Höhenstrahlung in konstanten Mengen gebildet wird und nach Verteilung über den ganzen Luftraum in gleich bleibender Konzentration vorhanden ist. Diese Annahme erwies sich bald als falsch, weshalb man nach Möglichkeiten einer Kalibration suchte. Diese ergab sich durch eine „endlose“ Dendrokurve, aus der in konstanten Jahrringabständen Proben auf ¹⁴C analysiert wurden.

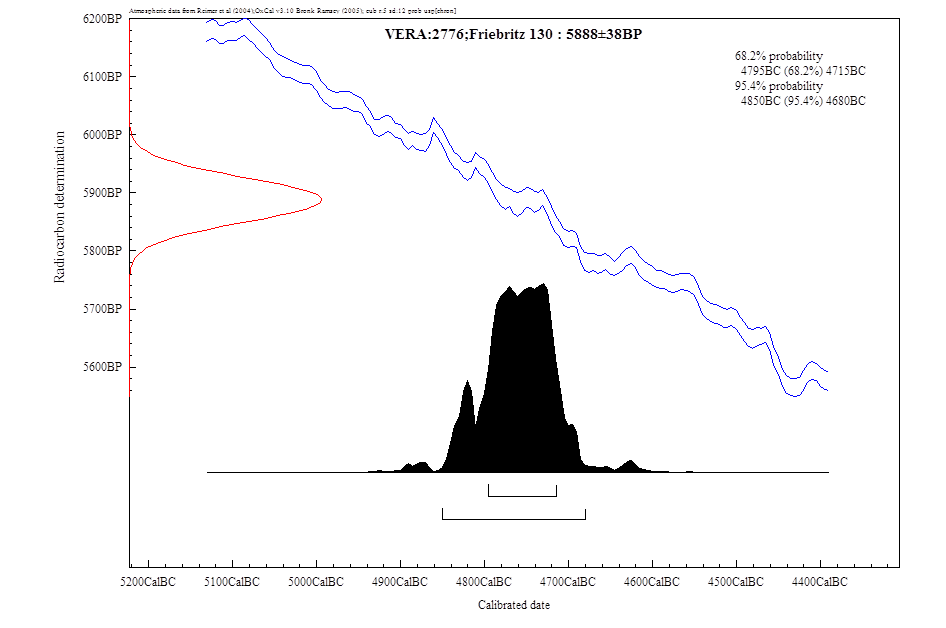
Das Ergebnis der Kalibration für dieses gerade besprochene¹⁴C-Messergebnis zeigt Abbildung 1, produziert mit Oxcal 3.10.

Auf der x-Achse sind die kalibrierten, also dem realen zeitlichem Verlauf entsprechenden Jahre CalBC aufgetragen. Auf der y-Achse sind die Werte BP, also die Messergebnisse aufgetragen, die Messung selbst entspricht einer Gauß’schen Glockenkurve (in der Grafik die rote Linie), wobei sich die Breite des Kurve nach dem Messfehler der Messung richtet, in unserem Fall also ± 38. Diese Verteilungskurve wird nun auf die unregelmäßig gezackte Kalibrationskurve projiziert und ergibt dann die ebenfalls unregelmäßige Verteilung nach der Kalibration, die deutlich als schwarz gefüllte Fläche zu erkennen ist. Rechts oben sind auf der Grafik zwei Kalibrationslösungen angegeben: zuerst auf dem 1-σ-Niveau (das entspricht 68,2%), in unserem Beispiel mit einer Lösung, von 4795-4715 v. Chr. Darunter dann das größere Intervall auf dem 2-σ-Niveau (entspricht 95,4%), im Beispiel 4850-4680 v. Chr.

Abb.1 Kalibration des ¹⁴C-Messergebnisses für Friebritz Grab Verfärbung 130 mit Oxcal 3.10.

Bei der weiteren Auswertung der ¹⁴C-Daten wurde das „Sequencing“ angewendet, ein immer häufiger eingesetztes Verfahren der Anwendung der Bayes’ischen Statistik. Da für viele Archäologen dieses Verfahren nicht selbstverständlich erscheint, möchte ich hier mit Hilfe von Grafiken, die Franz Weninger 2011 im Rahmen seiner Dissertation bei Walter Kutschera erstellt hat, das Verfahren ein wenig besser erklären.

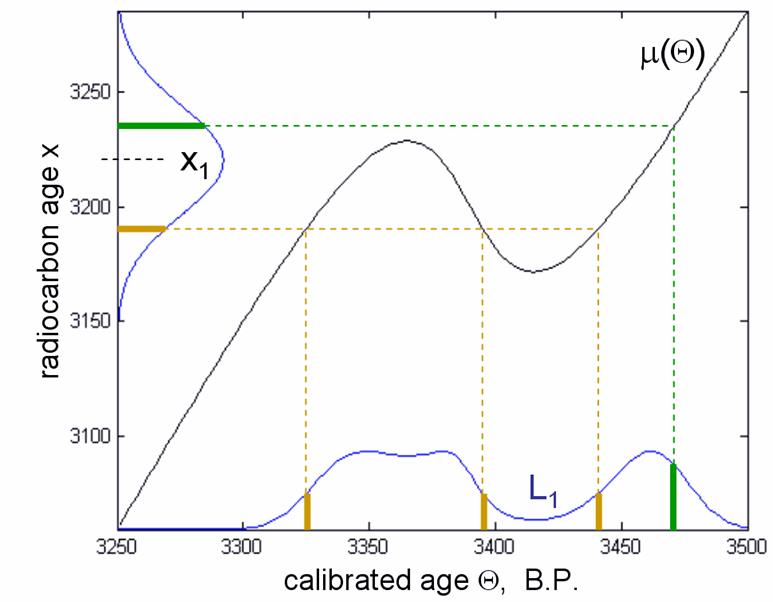
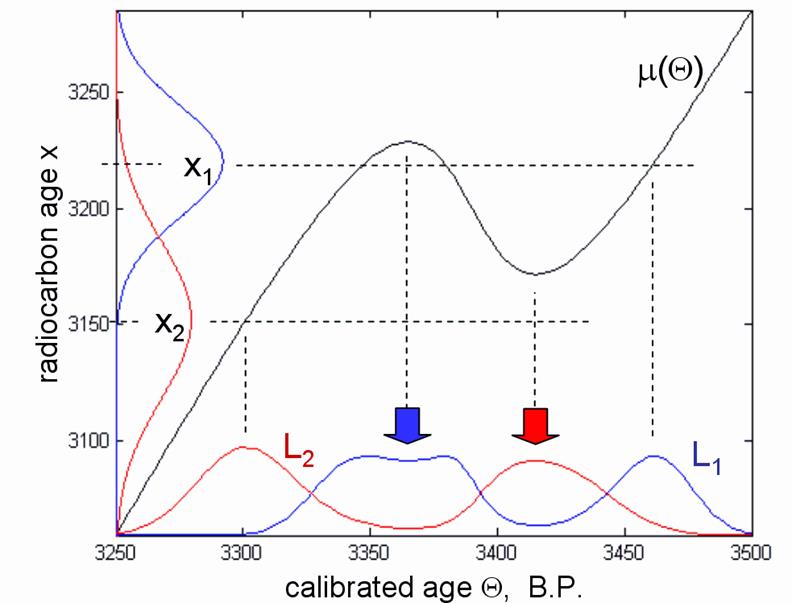
Nehmen wir in Abbildung 2 an, dass wir ein gemessenes Radiokarbonalter x₁ haben, mit einer Verteilungskurve in Form einer Glockenkurve (blaue Linie links oben). Die Wahrscheinlichkeitsfunktion L1 zeigt (blaue Linie unten), wie gut ein bestimmtes Kalenderjahr zum gemessenen Wert x1 passt. Praktisch wird diese Funktion produziert, indem man jeden Wert der Gauß’schen Glockenkurve zunächst horizontal auf die Kalibrationskurve projiziert und die Linie im rechten Winkel nach unten ablenkt (grünes Beispiel). Die Höhe unter der Glockenkurve entspricht dann der Höhe der Wahrscheinlichkeitsfunktion L₁. Dabei können auch mehrere Schnitte mit der Kalibrationskurve auftreten (braunes Beispiel), für jeden erhält die Wahrscheinlichkeitsfunktion dengleichen Wert.

Abb.2 Kalibration eines ¹⁴C-Messergebnisses an einer fiktiven Kalibrationskurve.

Beschreibung: 01

In Abbildung 3 ist die Kalibration zweier Proben mit dem Radiokarbonalter x₁(als blaue Kurve links)und x₂(rote Kurve links in der Abbildung) und der zusätzlichen Information dargestellt, dass Probe 1 jünger als Probe 2 ist. Durch unabhängige Kalibrierung erhalten wir zwei Wahrscheinlichkeitsfunktionen L₁ und L₂, dargestellt als rote und blaue Kurven unten. Offensichtlich stimmen nur die mit Pfeilen markierten Gipfel mit der angenommenen chronologischen Reihenfolge überein. Die Bayes’sche Methode kann mit solchen zusätzlichen Informationen in einer allgemeinen mathematischen Weise umgehen.

Abb.3 Kalibration zweier Proben, von denen eine Nebenbedingung bekannt ist, nämlich Probe x1 ist jünger als x2.

Beschreibung: 02

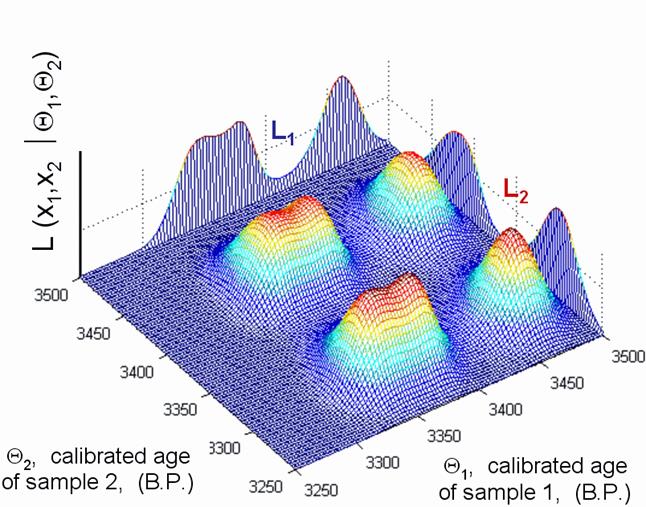
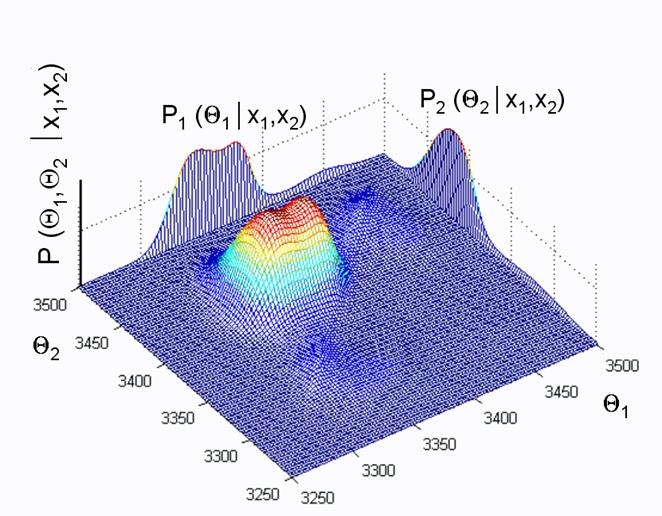
Die mehrdimensionale Wahrscheinlichkeitsfunktion L in Abbildung 4 ist das Produkt aller Einzel-Probenwahrscheinlichkeitsfunktionen. Dieses Produkt wird in einem mathematischen Raum berechnet. Seine Dimension ist die Zahl der Proben +1 (drei in diesem Beispiel).

Abb. 4 Die mehrdimensionale Wahrscheinlichkeitsfunktion.

Beschreibung: 03

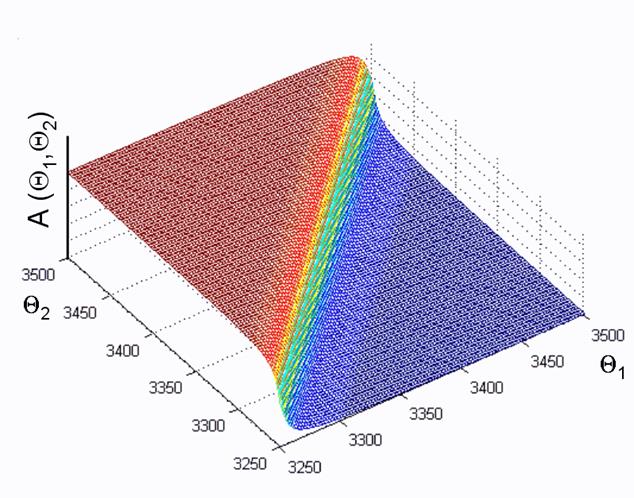
Die „Prior“ Wahrscheinlichkeit A in Abbildung 5 enthält die vorhandenen zusätzlichen Informationen über das zutreffende Alter Q₁ und Q₂. In unserem Beispiel weiß man, dass Probe 1 jünger als Probe 2 ist. So ist die „Prior“ Wahrscheinlichkeit hoch, wenn Q₁ < Q₂ (links von der Diagonale) und andererseits niedrig (rechte Seite).

Abb. 5 Die mehrdimensionale „Prior“ Wahrscheinlichkeit.

Beschreibung: 04

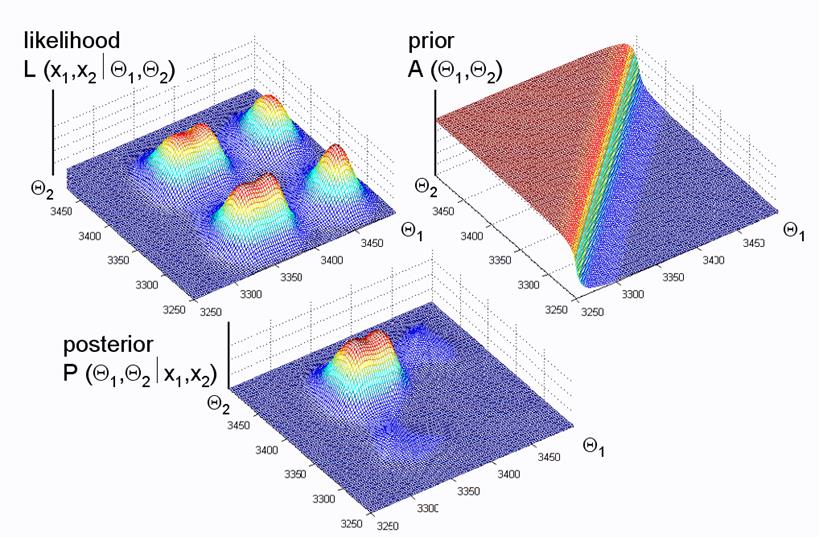
In Abbildung 6 links oben haben wir die gleichen Ausgangsbedingungen wie in Abbildung 4. Nun wird die Wahrscheinlichkeit in der linken Grafik Punkt für Punkt mit der rechts dargestellten Prior-Wahrscheinlichkeit multipliziert. Als Resultat erhalten wir die Abbildung 6 unten. Von den ursprünglich vier vorhandenen Lösungsgipfeln ist jetzt nur mehr die Lösung übrig geblieben, für die gilt, Probe 1 ist jünger als Probe 2.

Abb.6 „Posteriore“ Wahrscheinlichkeit ~ Wahrscheinlichkeit * „Prior“ Wahrscheinlichkeit = Bayes’sches Gesetz.

Beschreibung: 05

Projiziert man in Abbildung 7 den nun verbliebenen Lösungsgipfel einmal auf die eine Wandfläche, dann auf die andere, dann erhält man die marginalen (= randlichen) „Posterior“-Wahrscheinlichkeiten. Das sind die Lösungen, die man dann auch mit Oxcal erhält und die die reduzierten Datierungsintervalle widerspiegeln. Denn nur für diese sind die Nebenbedingungen erfüllt, dass Probe 1 jünger als Probe 2 ist.

Abb. 7 Die marginalen „Posterior“ Wahrscheinlichkeiten.

Beschreibung: 06

VERA= Vienna Environmental Research Accelerator.

Christopher Bronk Ramsey 1995, Radiocarbon Calibration and Analysis of Stratigraphy: The OxCal Program Radiocarbon 37/2, 425-430. Christopher Bronk Ramsey 2001, Development of the Radiocarbon Program OxCal, Radiocarbon, 43 (2A), 2, 355-363.

Als Kalibrationskurve wurde der atmosphärische Datensatz von Paula Reimer et al. 2004 Radiocarbon 46, 1029-1058, verwendet.

Gemeint ist damit vor 1950. Es wird also jedes ¹⁴C-Messergebnis auf das Jahr vor 1950 umgerechnet.

Thomas R. Bayes 1763, An essay Towards Solving A Problem In The Doctrine Of Chances. Philosophical Transactions of the Royal Society 53, 370-418.

Das „Wiggle Matching“.

Dem Dendrochronologen sehr geläufig und dennoch umstritten ist das „wiggle matching“, bei dem man ¹⁴C-Proben aus einer so genannten „floating chronology“ in wohl definierten Jahrringabständen nimmt. Im Fall vieler Dendrochronologien, die nicht bis heute laufen, ist das die einzige Möglichkeit zu einer Absolutchronologie zu gelangen. Umstritten ist das Verfahren, da man ja ¹⁴C-Daten mit einer ¹⁴C-datierten Standard-Dendrokurve (der Kalibrationskurve) kalibriert, um eine andere Dendrokurve letztlich zu datieren. Dabei beißt sich die Katze sozusagen in den Schwanz. Denn die gegenseitige Abhängigkeit von Dendrochronologie und ¹⁴C wird hier ganz offensichtlich.

Für die „floating dendrochronology“ lässt sich nun direkt kein Beweis führen, zu groß ist die Abhängigkeit von ¹⁴C-Datierung und Kalibrationskurve.

Andererseits kann man aus Analogiegründen eine bis in die Jetztzeit laufende Dendrochronologie testen. Unter anderem wurde so eine Untersuchung für die 7000 Jahre zurückreichende Zirbenchronologie von Kurt Nicolussi (Innsbruck) in Zusammenarbeit mit Walter Kutschera (VERA) durchgeführt. Zu dem Zweck wurde ein 500-jähriger Abschnitt aus dem dritten Jahrtausend vor Christus aus der Zirben-Dendrokurve alle 10 Jahre beprobt und mittels AMS ¹⁴C datiert. Die dabei zur normalen Kalibrationskurve festgestellten Abweichungen erwiesen sich als minimal und können aufgrund der Tatsache, dass die Eichen der ¹⁴C-Kalibrationskurve auf Meereshöhe und die Zirben an der Waldgrenze wachsen, auf die unterschiedlichen Hauptwachstumszeiten dieser Bäume und die saisonale Schwankung der ¹⁴C-Produktion zurückgeführt werden.

Nun zu einem Beispiel, bei dem man versucht, Eichenbretter aus einem awarenzeitlichen Brunnen, die von Otto Cichocki dendrodatiert wurden, mittels ¹⁴C und „wiggle matching“ zu überprüfen.

Für das Programm OxCal kann man einen Job schreiben, der folgendermaßen aussieht.

Texttabelle 8, „wiggle matching“ zweier Bretter aus dem awarenzeitlichen Brunnen von Brunn am Gebirge.

D_SEQ "Brunn, Awarischer Brunnen 823, Bretter 12 u.13,WM"

{

DATE "VERA262 :541 bis 551=546,0" 1485 35; GAP 50.0;

DATE "VERA263 :591 bis 601=596,0" 1410 35; GAP 4.5;

DATE "VERA265 :593 bis 608=600,5" 1485 40; GAP 32.5;

DATE "VERA266 :623 bis 643=633,0" 1425 35; GAP 22.5;

DATE "VERA267 :650 bis 663=656,5" 1350 35; GAP 4.5;

DATE "VERA264 :651 bis 671=661,0" 1275 35;

};

Die Zahlen nach der Labornummer sind der erste und der letzte Jahrring der Probe, danach steht der Mittelwert. Diese Werte stehen zusammen mit der Labornummer im Kommentar und werden für die weiteren Auswertungen nicht verwendet. Danach folgen die ¹⁴C-Messergebnisse in Jahren BP und der 1-σ-Fehler des Messergebnisses, dann folgt nach dem Stichwort „GAP“ der Jahrringabstand der Probenmittelwerte. Sie ergeben sich als Abstand des Mittelwertes in der gleichen Zeile zu dem in der nächsten Zeile. Vom Programm OxCal aus sind mittlerweile auch Dezimalzahlen möglich, da ja auch halbe Jahre bei den Mittelwerten auftreten können.

Das Kalibrationsergebnis dieses Jobs sieht man in der folgenden Textabbildung 27.

Textabbildung 27 Kalibration der Ergebnisse der Bretter 12 und 13 des awarenzeitlichen Brunnens von Brunn am Gebirge.

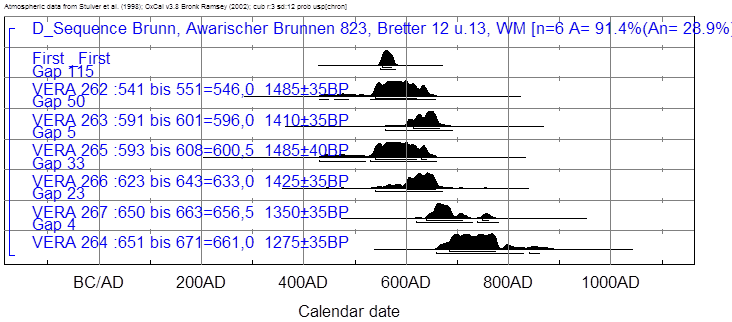
Hier folgt nun in Textabbildung 28 das „wiggle matching“. Dazu gibt es in oberer Textabbildung 27 den Korrelationskoeffizienten A=91,4%, der größer sein müsste als 28,9% um ein signifikantes Ergebnis zu liefern. Das ist bei weitem erfüllt.

Textabbildung 28, Wiggle Matching der Ergebnisse der Bretter 12 u.13 des awarenzeitlichen Brunnens von Brunn am Gebirge.

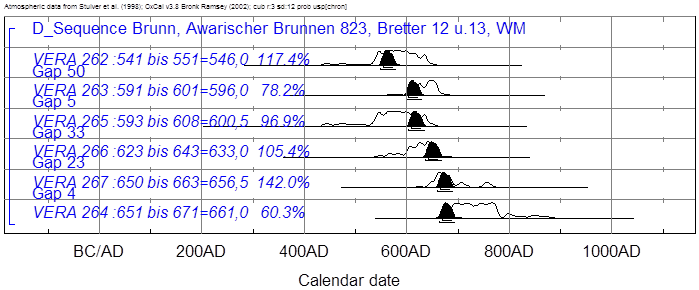
In diesem Fall versucht das Programm optimale Lösungen für die schwarzen Flächen innerhalb der weißen Flächen der Gesamtkalibration so auszuwählen, dass die Jahrringabstände der Proben als Randbedingungen erfüllt sind. Die Proben VERA-263 und VERA-265 liegen im Mittel nur 4,5 Jahre auseinander, deshalb wird für beide eine ziemlich gleiche Lösung ausgewählt. Probe VERA-262 ist jedoch 50 Jahre älter als VERA-263, somit wird auch eine ca. 50 Jahre ältere Lösung ausgesucht.

Für alle Proben wird eine Lösung erhalten, die zumindest zu mehr als 60,3% mit der einfachen Kalibration übereinstimmt. Dabei werden auch Werte bis zu 142% erhalten. 100% erhält man, wenn die schwarze Fläche gleich der weißen ist. Werte über 100 % können erhalten werden, wenn die schwarze Fläche mit der weißen Fläche nur in ihrem höchsten Teil überlappt. Proben, die weniger als 60% „agreement index“ haben, müssen in ihrem Jahrringabstand in Frage gestellt werden. D. h. man kann so auch Fehler in der Dendrochronologie, also Fehler bei der Überlappung der Bretter erkennen, was in unserem Beispiel jedoch nicht der Fall ist.

Nun zur Datierung der jüngsten Probe:

Textabbildung 29, Wiggle Matching der jüngsten Probe des
awarenzeitlichen Brunnens von Brunn am Gebirge.

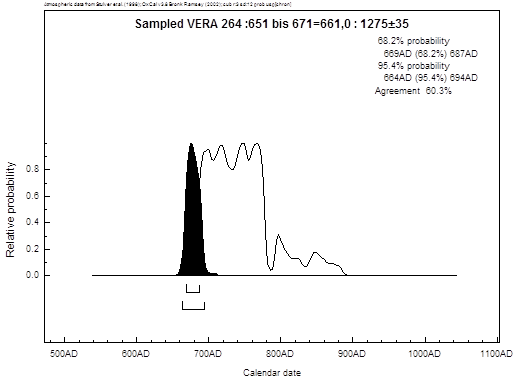
Der Bereich der schwarzen Fläche auf dem 1-σ-Niveau reicht von 669-687 AD. Damit liegt der zu erwartende Mittelwert für die dendrochronologische Altersbestimmung von 661 AD um mindestens 8 Jahre außerhalb dieses Intervalls. Nimmt man das 2-σ-Niveau, dann ist sie immerhin noch um mindestens 3 Jahre daneben.

An und für sich könnte man mit so geringen Abweichungen zufrieden sein. Es scheint, dass die „floating dendrochronology” der beiden Bretter von Brunn richtig ist, dass jedoch vielleicht Probleme beim Einpassen in die Deutsche Eichenkurve eine mögliche Ursache der Diskrepanzen sein könnten. Andererseits könnte die nicht berücksichtigte Jahrringverteilung innerhalb der Proben - d. h. eventuell haben die äußeren Jahrringe einen höheren Anteil - eine Rolle spielen. Jedenfalls scheint die „floating dendrochronology“, also die Verbindung von Brett 12 und 18 problemlos mit dem „wiggle matching“ in Einklang zu bringen zu sein.

Kann man den Mann vom Hauslabjoch (Ice man) noch genauer datieren?

Wie wir oben gesehen haben, kann der „Ice man = Eismann“ trotz zahlreicher Einzelmessungen nicht genauer datiert werden. Auch nach der Kombinationskalibration bleiben drei gleichwertige Lösungen über, die eine um 3300 v. Chr., die zweite ca. um 3200 und die dritte um 3150 v. Chr.

Nun kann man versuchen, die Proben des Eismannes in zwei Gruppen zu klassifizieren, in ältere und jüngere aufgrund des datierten Materials. Denn das Knochenkollagen sollte auch beim Eismann, der ein Lebensalter von 40-45 Jahre Jahren ereichte, um einiges älter sein als die jüngeren, „kurzlebigen“ Gräser vom Mantel, von den Schuhen und der Köcherversteifung, ebenso wie seine Haare.

Tatsächlich erhält man unterschiedliche Ergebnisse bei den Kombinationskalibrationen.

Textabbildung 30, Kombinationskalibration der älteren Proben vom Mann vom Hauslabjoch (Eismann).

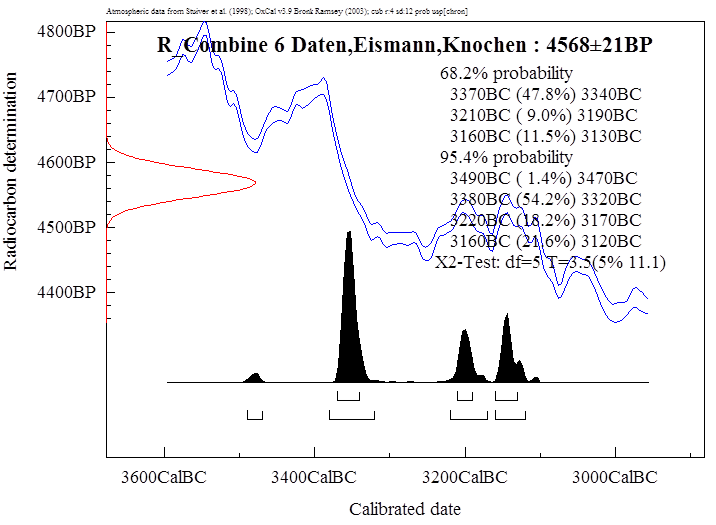
Die Lösung in Textabbildung 30 favorisiert schon die älteste Lösung um etwa 3350 v. Chr.

Textabbildung 31, Kombinationskalibration der jüngeren Proben vom Mann vom Hauslabjoch (Eismann).

D. h. zweifelsfrei ist das Knochenkollagen älter, der Unterschied im unkalibrierten ¹⁴C-Alter beträgt im Mittel 51 Jahre. Nach der Kalibration erhalten wir wieder 3 Lösungen, von denen keine bevorzugt werden darf. 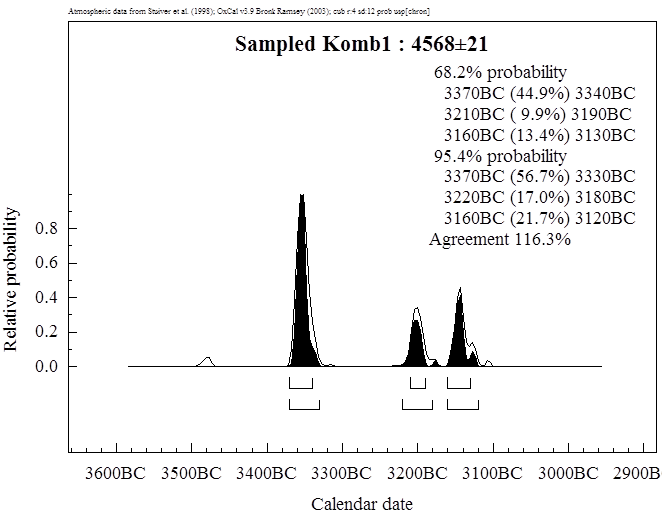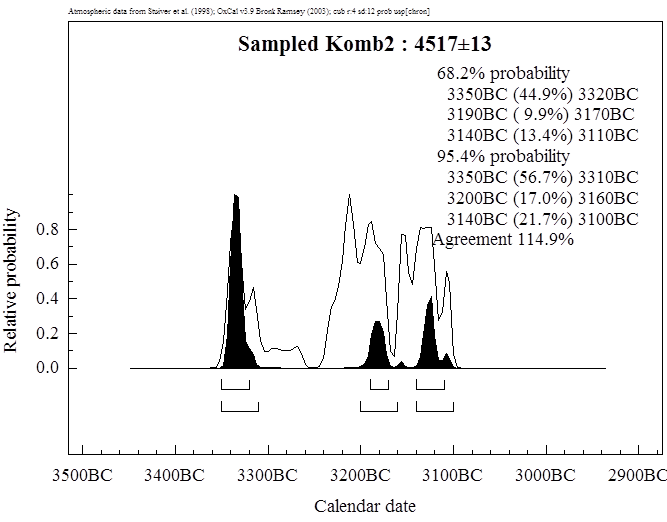Wenn man die gleichen Untersuchungen nur mit den Proben macht, die wirklich vom menschlichen Körper stammen, also Messungen von Knochen, Haut und Haaren, jeweils also 6 Proben (in der Tabelle auf der DVD-R in der zweiten Spalte Phasen2), dann erhält man für die älteren Proben 4568±21, für die jüngeren 4503±22, also eine noch größere Differenz von 65 Jahren.

Wir können nun versuchen, das Lebensalter in unsere Betrachtungen mit einzubeziehen. Der „Abstand“ zwischen Kollagen und Haaren sollte bei einem Alter von 40 Jahren etwa 20 Jahre betragen, bei 45 Jahren etwa 25 Jahre. Sehen wir uns nun mehrere „wiggle matchings“ mit Altersabständen zwischen Kollagen und Haaren von 15, 20 und 25 Jahren an. Diese drei Abstände werden getestet, da nicht wirklich klar ist, in welchem genauen Zusammenhang der Abstand zum Sterbealter steht und ja auch das Sterbealter zwischen 40 und 45 Jahren liegt.

Textabbildung 32, WM mit Abstand 15, 20 und 25 Jahren.

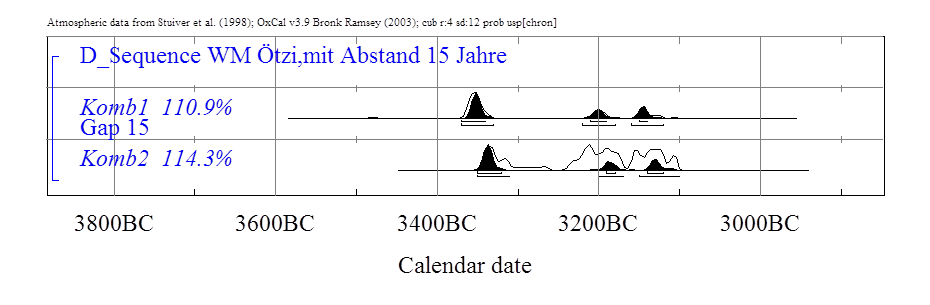
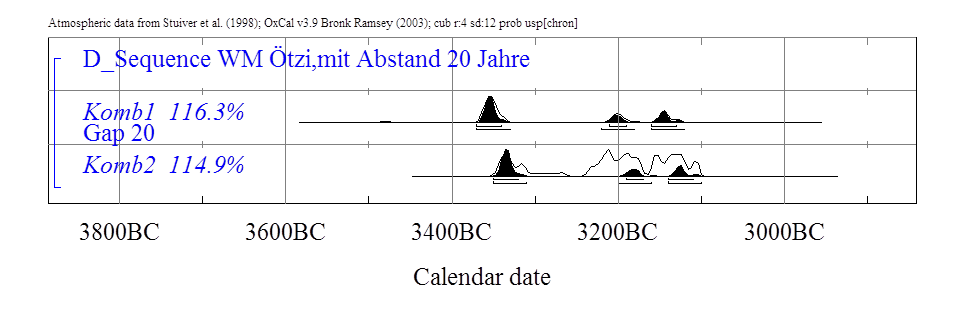
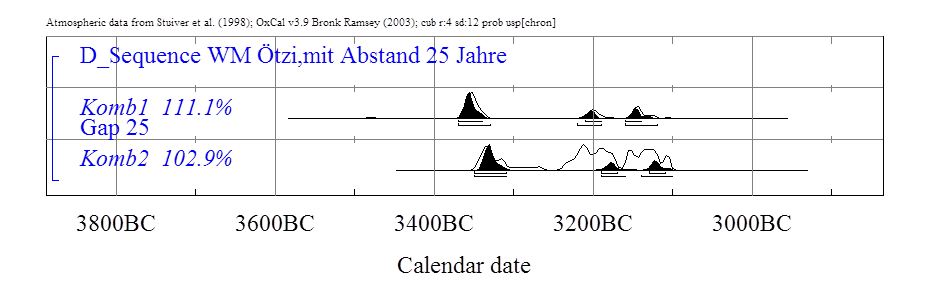
Im Allgemeinen sind die drei Lösungen sehr ähnlich und favorisieren die älteste Datierung für den Eismann. Wir erhalten bei einem zeitlichen Abstand von 20 Jahren für das zwanzigste Jahr des Eismannes, das Jahr aus dem das Kollagen stammt, ein Datierungsintervall von 3370-3340 auf dem 1-σ-Niveau. Für das vierzigste Jahr ergibt sich ein Intervall von 3350-3320. Wenn wir das Leben des Eismannes insgesamt bestimmen wollen, dann von 3390-3360 als Intervall für seine Geburt und von 3350-3320 v. Chr. für seinen Tod.

Die folgenden Textabbildung 33-35 zeigen den gleichen Sachverhalt noch in Form von Einzelkalibrationen. Wie wir aus den Grafiken erkennen, verbleibt eine statistisch sehr geringe Möglichkeit von 9,9% bzw. 13,4% für die beiden späteren Datierungen. Gegenüber der „normalen“ Kombinationskalibration, in der alle drei Lösungen ziemlich gleich gewichtet waren, ist das jedoch ein enormer Fortschritt.

Textabbildung 33, Datierung des 20. Lebensjahres des Eismannes durch Kollagen unter Voraussetzung eines 20-jährigen Abstandes.

Textabbildung 34, Datierung des 40. Lebensjahres des Eismannes durch Haare, Gras etc. unter Voraussetzung eines 20-jährigen Abstandes.

Texttabelle 9, Datierung des Eismannes unter Annahme eines 20-jährigen Abstandes zwischen Kollagen und Haaren.

	Intervall im 1-σ-Bereich
Jahr	Beginn	Ende
Geburt	3390	3360
20. Lebensjahr	3370	3340
40. Lebensjahr=Tod	3350	3320

Macht man das „Sequencing“ nur mit den Proben vom menschlichen Körper, erhält man genauso die Favorisierung der ältestmöglichen Datierung, die Wahrscheinlichkeit der anderen Datierungen ist jedoch aufgrund der geringeren statistischen Sicherheit bei der kleineren Probenzahl etwas größer als zuvor.

Diese Ergebnisse stehen nun im Gegensatz zu unseren früheren Vermutungen, dass ein „Event“ um ungefähr 3200 v. Chr. mit der Überdeckung des Eismannes mit Schnee und Eis in Zusammenhang stehen könnte.

Eine Möglichkeit, diese Frage von einem anderen Blickwinkel anzugehen, könnten die Jahrringe des Eibenbogens bringen, der zusammen mit dem Eismann gefunden wurde. Wenn hier mehr als 60-80 Jahrringe bei der dünnwüchsigen Eibe zu erwarten wären, könnte damit ebenfalls ein „wiggle matching“ zu einer Bestätigung unserer hier präsentierten Datierung ermöglichen.

Nun wenden wir uns einem Beispiel aus unserem SCIEM2000 Projektbereich zu.

Beschreibung: http://www.nhm-wien.ac.at/SCIEM2000/Images/logo_main.gif

Sequencing

Simulation der Datierung der Aschenschichte der Santorineruption im Pollenprofil von Gölhisar Gölü mit ¹⁴C und „Sequencing“.

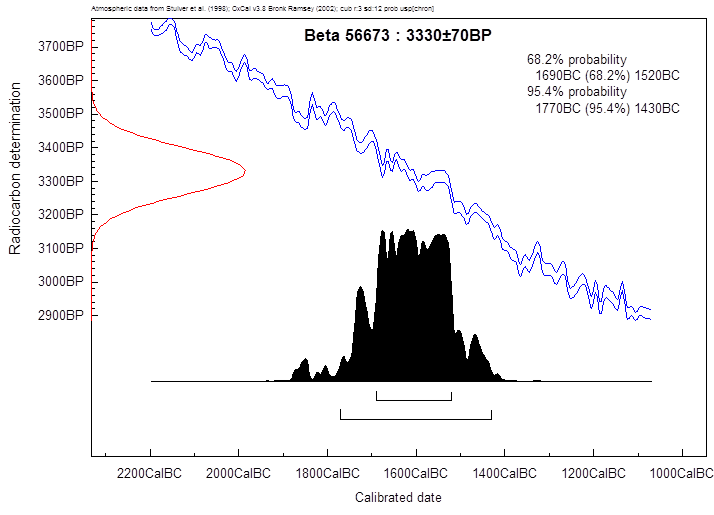
Die Publikation des Pollenprofiles durch Eastwood et al. gibt in unmittelbarem Bereich der Schicht mit der Thera-Eruptions-Asche ein ¹⁴C-Datum von 3330 ± 70 BP an, dort kalibriert mit ~ 1600 BC. Die folgende Abbildung zeigt das Kalibrationsergebnis. Tatsächlich erhält man auf dem 1-σ-Niveau ein Intervall von 1690-1520, siehe Textabbildung 35. D. h. sowohl die naturwissenschaftliche als auch die historische Datierung wären danach also möglich.

Textabbildung 35, Einzelkalibration der Aschenschicht von Gölhisar Gölü.

Vorausschickend soll gleich angemerkt werden, dass das hier angewandte Verfahren zwar mit dem „wiggle matching“ verwandt ist, jedoch im Allgemeinen in der Fachliteratur mit anderen Namen wie „Sequencing“ oder „Sequence“ bedacht ist.

Simulationen bieten sich immer dann an, wenn noch keine oder nicht ausreichend Messungen gemacht wurden und wenn man ermitteln will, welche die optimale Probenkonstellation sein könnte. Mit OxCal wurden mehrere Simulationen durchgeführt, um die kostengünstigste Variante unter möglichster Optimierung der Genauigkeit des Ergebnisses zu ermitteln.

Dabei zeigt sich eine Zahl von 11 Proben als ausreichend. 5 Proben oberhalb der Schicht, 5 Proben unterhalb und eine in der Schicht sollten möglichst im Abstand von ca. 10 Jahren von einander ausgewählt werden. Damit wäre der Abstand zwischen oberster und unterster Probe mit ca. 100 Jahren zu veranschlagen. Das bedeutet im Profil GHA ca. 8-10 cm. D. h. die Proben sollten ca. alle 1 cm beginnend 5 cm unterhalb der Aschenschicht bis 5 cm oberhalb gezogen werden. Die Sedimentationsrate kann als ziemlich gleichmäßig angesehen werden, in 10000 Jahren BP wurden etwa 800 cm Sedimentation erreicht, also ca. 12,5 Jahre/cm. Diese Information über den zeitlichen Abstand, die ja nur eine Schätzung ist, fließt nicht ein in die weiteren Berechnungen.

Die Proben müssten dann mittels Hochpräzisions-AMS (σ ca. 20a) gemessen werden, was bei VERA möglich wäre, da ja auch die Zirbenholzkalibrationskurve nach diesem Prinzip bestimmt wurde.

Die Ergebnisse dieser Simulation sehen folgendermaßen aus. Die Tests wurden zunächst unter der Voraussetzung der Richtigkeit des naturwissenschaftlichen Datierungsansatzes der Thera-Eruption gemacht.

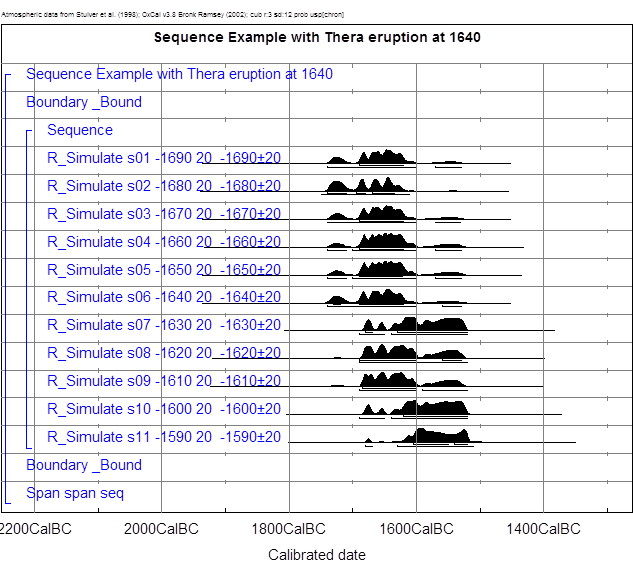
Zunächst das Job-File in Textabbildung 10, mit dem in OxCal diese Auswertungen vorgenommen werden können:

Texttabelle 10, Job-File für die Simulation des Thera-Ausbruchs um 1640 v. Chr.

Sequence "Beispiel mit Thera-Ausbruch um 1640"
{
    Boundary;
    Sequence
    {
    R_Simulate "s01 -1690 20" -1690 20;
    R_Simulate "s02 -1680 20" -1680 20;
    R_Simulate "s03 -1670 20" -1670 20;
    R_Simulate "s04 -1660 20" -1660 20;
    R_Simulate "s05 -1650 20" -1650 20;
    !Thera-Ausbruch
    R_Simulate "s06 -1640 20" -1640 20;
    !Thera-Ausbruch
    R_Simulate "s07 -1630 20" -1630 20;
    R_Simulate "s08 -1620 20" -1620 20;
    R_Simulate "s09 -1610 20" -1610 20;
    R_Simulate "s10 -1600 20" -1600 20;
    R_Simulate "s11 -1590 20" -1590 20;
    };
    Boundary;

Span "span seq";
};

Die Prozedur R_Simulate produziert dabei simulierte ¹⁴C-Messergebnisse, die nach ihrer Verteilung rund um den Mittelwert bei vorgegebenem Messfehler tatsächlich realen ¹⁴C-Datierungen sehr nahe kommen. Dazu kommt, dass bedingt durch ein jeweils unterschiedliches „seed“ für den Zufallszahlengenerator bei jeder weiteren Berechnung unterschiedliche Resultate erhalten werden, was der Realität entspricht, denn auch bei jeder neuen Messung werden unterschiedliche Resultate erzielt, allerdings genauso definiert durch den wahren Mittelwert und den Messfehler. In den folgenden beiden Textabbildungen 36 und 37 und sehen wir zunächst die Kalibration und das Sequencing der simulierten Daten.

Textabbildung 36, Gölhisar Gölü, Kalibration, mit präsumtivem Thera-Ausbruch um 1640 BC.

Textabbildung 37, Gölhisar Gölü, WM, mit präsumtivem Thera-Ausbruch um 1640 BC.

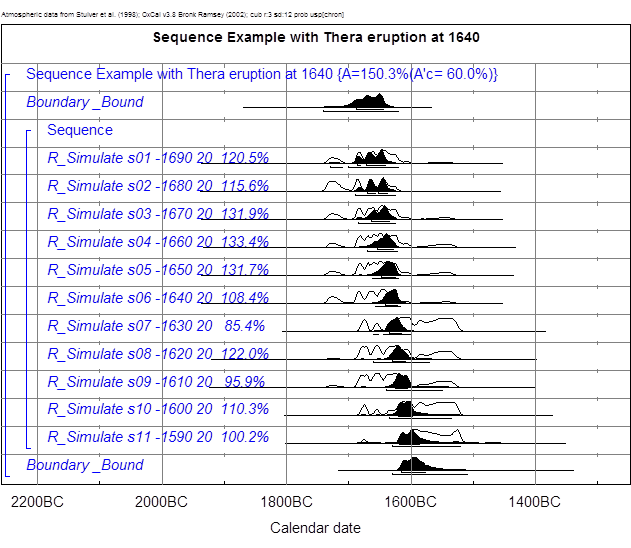
Die Einzelprobe aus dieser Serie, die am nächsten bei der Eruption liegt (1640 BC) würde folgendermaßen kalibriert werden: auf dem 1-σ-Niveau von 1730-1620 BC. Die zugehörigen Grafiken sind in der Textabbildung 38 und 39 zu sehen.

Textabbildung 38, WM Gölhisar Gölü, Kalibration der Einzelprobe zum Ausbruch, mit präsumtivem Thera-Ausbruch um 1640 BC.

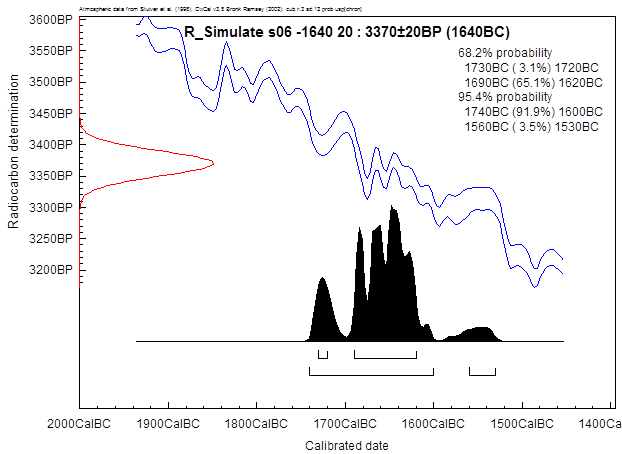
Das „sequencing“ dieser Probe liefert folgendes Ergebnis, die Einzelprobe aus dieser Serie, die am nächsten bei der Eruption liegt (1640 BC) würde durch das „Sequencing“ folgendermaßen datiert:

Textabbildung 39, WM Gölhisar Gölü, WM der Einzelprobe zum Ausbruch, mit präsumtivem Thera-Ausbruch um 1640 BC.

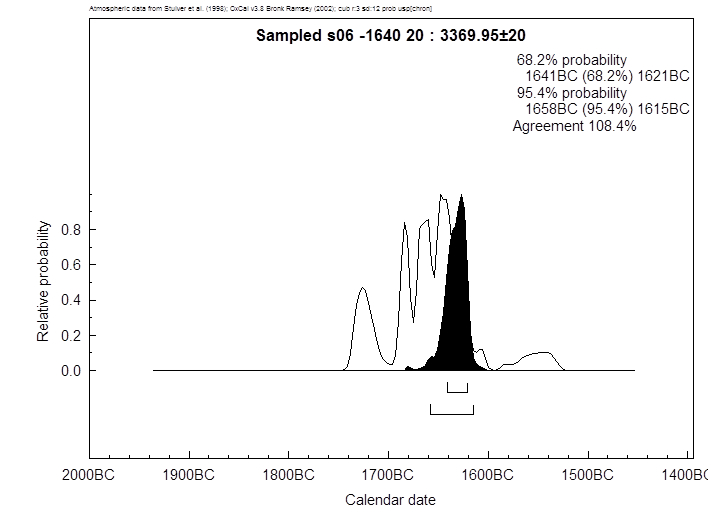
D. h. die schwarze – mit „Sequencing“ ermittelte- Fläche ergibt ein Intervall auf dem 1-σ-Niveau von 1641-1621, der „wahre“ Wert von 1640 liegt gerade innerhalb.

Warum funktioniert dieses Verfahren nun, obwohl hier keine Jahrringabstände eingehen? Denn die etwa zehn Jahre Abstand, die zwischen den hypothetischen Proben eingehalten werden, werden bei diesem Verfahren (sequence) nicht benutzt. Es wird lediglich die Reihenfolge der Proben verwendet. Programm OxCal mit seinem Gibbs-sampler optimiert nun die schwarzen Flächen unter den weißen Flächen unter Einhaltung der Randbedingungen, die da lauten: Alle Proben befinden sich in einer Sequenz, d. h. wenn man das Alter der Proben mit bis bezeichnet, gilt oder allgemein formuliert. Nun spielt hier bei der Optimierung natürlich die Lage der „wiggles“ in der Kalibrationskurve eine wichtige Rolle.

Nehmen wir die Probe genau um 1640 BC, siehe Textabbildung 39. Bei ihr ist die schwarze Fläche genau über dem letzten oder jüngsten höheren „wiggle“ der Einzelkalibration oder der weißen Fläche. Ein späteres „wiggle“ würde einen „agreement index“ unter 60% haben und damit die Sequenz in Frage stellen. Damit ist die schwarze Fläche sozusagen schon am spätestmöglichen wiggle angeordnet. Die nachfolgenden Proben haben in der einfachen Kalibration (weiße Fläche) weitere wiggles, die nun sukzessive für die weiteren schwarzen Flächen herangezogen werden können.

Nochmals zum Resultat des „Sequencing“ bei der zuletzt besprochenen Probe: Das Datierungsintervall kann durch das „Sequencing“ im 1-σ-Bereich von 1730-1620 auf 1658-1615 reduziert werden. Diese Genauigkeit kann bei anderen Konstellationen (mehr Proben, längerer Zeitraum etc.) kaum mehr unterboten werden. Für die Fragestellung, welche der beiden Chronologien die richtige ist, sollte sie jedoch bei weitem ausreichend sein.

Sollte die historische Datierung richtig sein, so würde das ganz analog funktionieren. Das soll im Weiteren gezeigt werden, mit einer angenommenen Datierung der Eruption um 1500. (Bei anderen Annahmen wäre das ebenfalls analog durchzuführen) Dazu wieder das entsprechende Job-File:

Texttabelle 11, Job-File für die Simulation des Thera-Ausbruchs um 1500 v. Chr.

Sequence "Beispiel mit Thera-Ausbruch um 1500"

{

Boundary;

Sequence

{

R_Simulate "s01 -1550 20" -1550 20;

R_Simulate "s02 -1540 20" -1540 20;

R_Simulate "s03 -1530 20" -1530 20;

R_Simulate "s04 -1520 20" -1520 20;

R_Simulate "s05 -1510 20" -1510 20;

! Thera-Ausbruch

R_Simulate "s06 -1500 20" -1500 20;

! Thera-Ausbruch

R_Simulate "s07 -1490 20" -1490 20;

R_Simulate "s08 -1480 20" -1480 20;

R_Simulate "s09 -1470 20" -1470 20;

R_Simulate "s10 -1460 20" -1460 20;

R_Simulate "s11 -1450 20" -1450 20;

};

Boundary;

Span "span seq";

};

Dazu nun die beiden Abbildungen Textabbildung 40 und 41.

Textabbildung 40, WM Gölhisar Gölü, Kalibration, mit präsumtiven Thera-Ausbruch um 1500 BC.

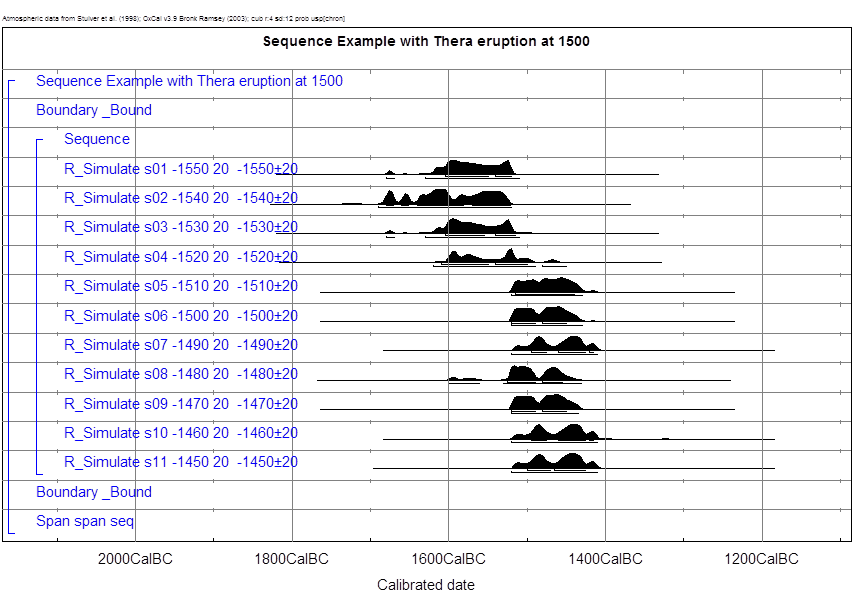
Textabbildung 41, WM Gölhisar Gölü, mit präsumtivem Thera-Ausbruch um 1500 BC.

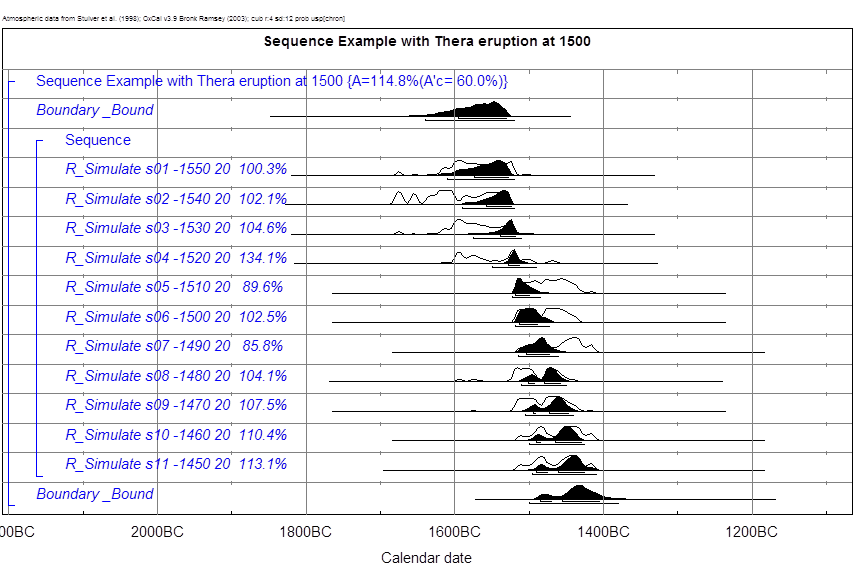
Die Einzelprobe aus dieser Serie, die am nächsten bei der Eruption liegt (1500 BC, nach der Ägyptischen Chronologie) ergibt bei der Einzelkalibration auf dem 1-σ-Niveau folgendes Intervall: 1520-1450 BC, siehe Textabbildung 42.

Textabbildung 42, Gölhisar Gölü, Kalibration, Einzelprobe vom Ausbruch, mit präsumtiven Thera-Ausbruch um 1500 BC.

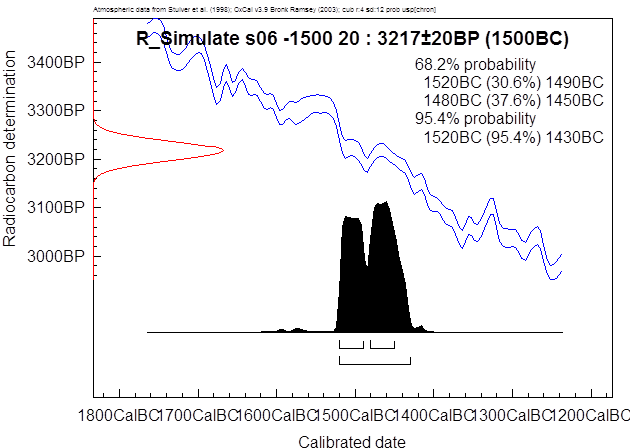
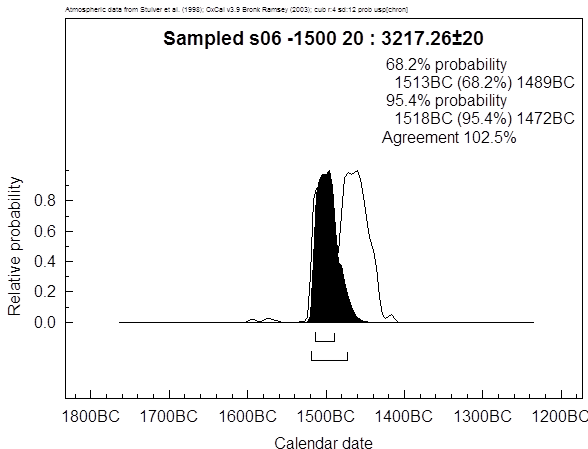
Dieses Intervall würde durch das wiggle matching weiter reduziert werden, und zwar auf 1513-1489 BC, siehe Textabbildung 43. Damit liegt der (erwartete) Wert von 1500 sowohl innerhalb des 1-σ- als auch klarerweise des 2-σ-Intervalls.

Textabbildung 43, Gölhisar Gölü, WM, Einzelprobe vom Ausbruch, mit präsumtiven Thera-Ausbruch um 1500 BC.

Variable „Sequence“.

Diese Form des „wiggle matching“ entspricht fast vollständig der einfachen Form mit Jahrringabständen mit dem Unterschied, dass zusätzlich zu dem Jahrringabstand auch ein σ für diesen Abstand angegeben werden kann. Das folgende Beispiel ist dem OxCal-Hilfe-File entnommen (siehe Texttabelle 12). Nach dem Eintrag Gap wird zuerst der Jahrringabstand angegeben, in unserem Beispiel mit 50, dann folgt das σ dieses Abstandes mit 10 Jahren.

Texttabelle 12, Beispiel einer variablen Sequenz mit σ für den Jahrringabstand.

V_Sequence "Beispiel Variable Sequence"

{

R_Simulate 0 30; Gap 50 10;

R_Simulate 50 30; Gap 50 10;

R_Simulate 100 30; Gap 50 10;

R_Simulate 150 30; Gap 50 10;

R_Simulate 200 30; Gap 50 10;

R_Simulate 250 30;

};

Meines Erachtens kann man das ideale Anwendungsgebiet dafür in der Dendrochronologie kaum finden, denn dort gibt es entweder sehr exakte oder sehr unterschiedliche Lösungen. Wenn dagegen eine „Sequence“ archäologischer Fundkomplexe von anderen Verfahren produziert wird, wie Seriation, Korrespondenzanalyse oder Analyse der N Nächsten Nachbarn, kann diese mit V_Sequence ausgewertet werden. Denn jedes mathematische Verfahren, dass eine „Sequence“ ermittelt, kann für die Fundkomplexe, aber auch die Typen ein σ angeben. Dazu muss man jedoch zunächst „hypothetische“ Jahrringabstände berechnen oder abschätzen und die Größe ihres Fehlers (das σ). Das kann nur gelingen, wenn man den gesamtzeitlichen Rahmen seiner Fundkomplexe kennt. Daraus lässt sich dann der SD/a-Koeffizient berechnen, nach folgender Formel:

dabei bedeutet:

Sequenzdaten pro Jahr, also der SD/a-Koeffizient.

der gesamte Bereich der Sequenzdaten, also bei WinSerion 1000 SD.

die Gesamtdauer in Jahren.

Da jedoch in den seltensten Fällen die Sequenzdaten äquidistant bezüglich der absoluten Jahrskala sind, dass heißt gleichen SD-Abständen gleiche Zeiträume entsprechen, kann das nur eine Annäherung an ein ideales Resultat sein. In einem Beispiel mit der awarischen Seriation weiter unten werden wir zeigen, wie man in solch einem Fall, unter Berechnung mehrerer SD/a-Koffizienten für verschiedene Sequenzdatenbereiche umgehen kann.

Ich hoffe damit gezeigt zu haben, dass ein „wiggle matching“ oder besser gesagt eine „sequence“ von ¹⁴C-Daten so gut kalibriert werden kann, dass dann eigentlich kaum mehr Zweifel an der Datierung verbleiben könnten.

BAYES Thomas 1764, An essay towards solving a problem in the doctrine of chances. Philosophical Transactions of the Royal Society 53, 370–418.

BRONK RAMSEY Christopher 2003, OxCal manual.

Hier eine einfache Einführung in Bayes’ Gesetz.

DELLINGER Franz, KUTSCHERA Walter, STEIER Peter, WILD Eva Maria, NICOLUSSI Kurt, SCHIESSLING Peter 2004, A ¹⁴C calibration with AMS from 3500 to 3000 BC, derived from a new high-elevation stone-pine tree-ring chronology. Radiocarbon, in press.

Das ist zumindest richtig für die letzte Version 3.10.

Zu ähnlichen Schlussfolgerungen und Ergebnissen kam Christopher Bronk-Ramsey anlässlich eines Vortrages in Wien im Jänner 2004. Wir wissen allerdings nicht, wie viele und welche Daten er benutzte.

Die Altersangabe verdanken wir Maria Teschler, die ja selbst den Eismann untersuchen konnte.

STADLER Peter, DRAXLER Susanne, FRIESINGER Herwig, KUTSCHERA Walter, PRILLER Alfred, ROM Werner, STEIER, Peter, WILD Eva 2000, Status of the Austrian Science Fund Project P 12253-PHY: Absolute Chronology for Early Civilisations in Austria and Central Europe using ¹⁴C Dating with Accelerator Mass Spectrometry. 35 Seiten, 28 Tabellen, 61 Abbildungen, Manuskript, 25-27.

The Synchronization of Civilizations in the Eastern Mediterranean in the 2nd Millennium BC. Projektsprecher des Sonderforschungsbereiches Univ. Prof. Dr. Manfred Bietak. Die Projekt Homepage befand sich hier: http://www.oeaw.ac.at/sciem2000/

EASTWOOD W.J., ROBERTS N., LAMB H. F., TIBBY J. C. 1999, Holocene environmental change in southwest Turkey: a palaeoecological record of lake and catchment-related changes. Quarternary Science Reviews 18, 671-695.

Letzte Bearbeitung 12.11.2018

Einführung in die Bayes’sche Statistik.