Grundbegriffe der Relativchronologie

Peter Stadler

Einleitung:

Für die Stellung der archäologischen Wissenschaft als Instrument der Geschichtsforschung ist die zeitliche Einordnung von archäologischen Funden von besonderer Bedeutung. Neben der weitgehend naturwissenschaftlich dominierten Ermittlung der Absolutchronologie spielt die der archäologischen Methodik eigene Relativchronologie dabei eine große Rolle.

Stratigraphie:

Für eine Relativchronologie liefert die Stratigraphie die härtesten Argumente. Man erkannte schon relativ bald die vertikal-stratigraphische Abfolge. Untenliegende Schichten sind - im Allgemeinen - älter als darüber liegende. Bis vor einigen Jahren wurden stratigrafische Zusammenhänge zunächst dokumentiert und dann auf dem Schreibtisch ausgewertet. Dabei auftretende Probleme konnten oft nicht mehr gelöst werden. Erst seit Entwicklung der HARRIS-Matrix, kann man von einer systematischen Dokumentation der Schichtenfolgen sprechen. Ein Computerprogramm ermöglicht es heute, gleich während der Grabung alle Zusammenhänge einzugeben und rein rechnerisch zu überprüfen und diese Probleme sofort aufzuzeigen und damit zu vermeiden. Näheres zu dieser Methode findet man hier:

Da jedoch nicht immer diese stratigraphischen Zusammenhänge auf europäischen Fundplätzen so gut beobachtbar sind wie an den Tell-Siedlungen mit ihren oft mehr als 10 m hohen Schichtenlagen, wurden schon sehr früh andere Methoden entwickelt, die ebenfalls zu einer Relativchronologie beitragen können.

Typologische Methode:

Der erste, der diese Methode anwandte, war THOMSEN, der die Relikte urgeschichtlicher Zeiten vor allem nach dem Material in Stein, Kupfer und Eisen unterschied und danach auch die einzelnen Abschnitte - eben in dieser zeitlichen Reihenfolge - benannte. Ganz klar als Methode wurde diese Vorgangsweise von MONTELIUS in seinem grundlegenden und auch heute immer noch angewandten Werk "Die Methode ..." formuliert.

Bild von Oscar Montelius:

Sein Ausgangspunkt in der Entwicklung dieser Methode war die typologische Reihe. Er griff einen bestimmten Gegenstand, zum Beispiel die Kupfer- und Bronzedolche Italiens heraus und sammelte alle Vertreter. Dann versuchte er, im Sinne einer sich in den Objekten niederschlagenden "Kultur-Evolution" die verschiedenen Exemplare dieses Gegenstands in eine Reihe zu bringen, die ihrer Entwicklung im Laufe der Zeit entsprechen könnte. Zu Anfang war nicht klar, in welcher Richtung diese Reihe läuft. Da hilft das sogenannte technologische Ornament weiter, das auch als typologisches Rudiment bezeichnet wird. MONTELIUS verstand darunter ein Gestaltelement, das jede Funktion verloren hatte, dessen Ableitung jedoch aus Vorstufen, in denen es noch eine Bedeutung hatte, möglich ist.

Waren nun für die verschiedenen Gegenstände, etwa Beile, Dolche und Schwerter diese Reihen aufgestellt, so konnte ihre Richtigkeit durch Parallelität bestätigt werden. Das bedeutet nun keineswegs, dass für verschiedene typologische Reihen das gleiche Tempo der Entwicklung vorausgesetzt werden kann. Dies bedeutet in unserem Beispiel folgendes:

1. A.....B.....C.D........E = Reihe für Schwerter

zeitlicher Verlauf

2. A..B....C..D.E.......F = Reihe für Beile

In dieser parallelisierten Typenentwicklung sieht man, dass die Geschwindigkeit der Entwicklung in beiden Reihen unterschiedlich sein kann. Mit annähernd großer Wahrscheinlichkeit wird das Schwert vom Typ A zumeist zusammen mit Beilen vom Typ A, selten vom Typ B, aber kaum mit C und D gefunden. Beil B jedoch tritt gleich häufig mit Schwert A und B auf.

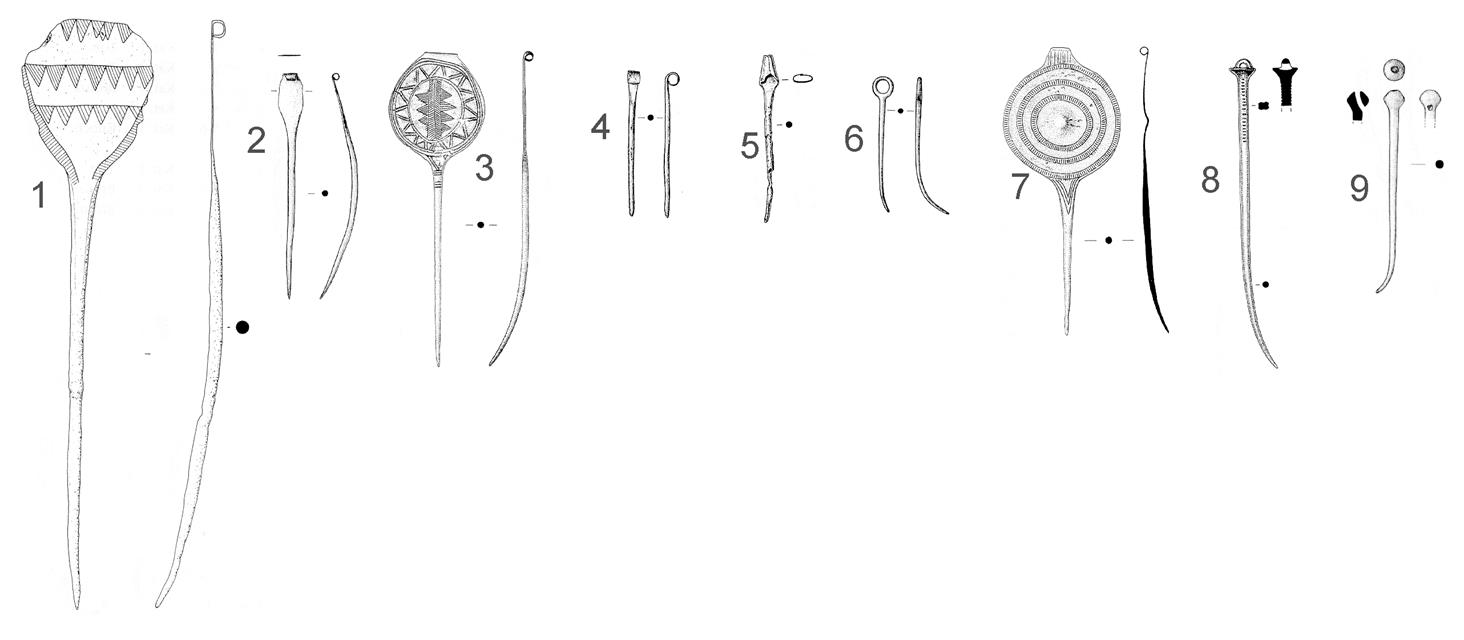
Ein anderes Beispiel: Frühbronzezeitliche Nadel-Typologie nach Johannes-Wolfgang Neugebauer:

Weiteres Beispiel: Frühbronzezeitliche Beil-Typologie, nach www.praehistorische-archaeologie.de:

Beispiel: Spätawarische Riemenzungen, nach Peter Stadler 1991a.

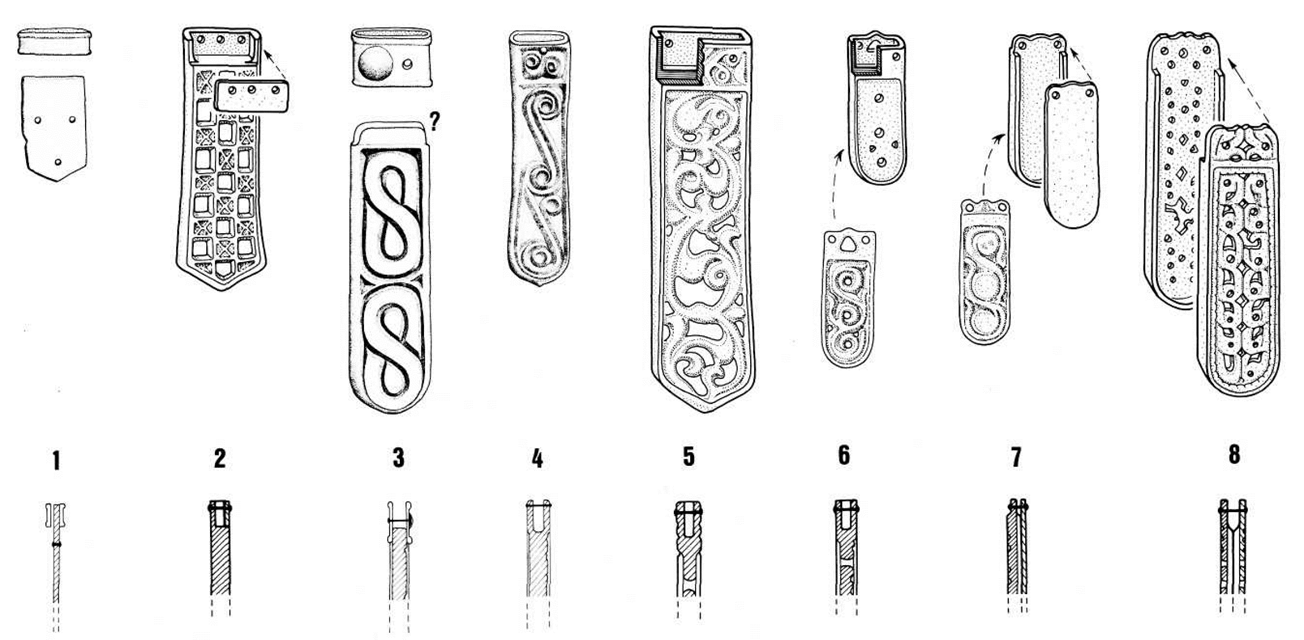
Die Typologische Methode verlangt eine außerordentliche Feinfühligkeit für die Typologie und ist - wie sich zum Leidwesen nachfolgender Forschergenerationen herausstellte - kaum in anderen als den von MONTELIUS ausgewählten Beispielen derartig konsequent durchführbar gewesen. Deshalb wurde bald nach einem anderen Hilfsmittel gesucht.

Kombinationsstatistik:

Es wurde in der kombinatorischen Methode gefunden. Ein Ausgangspunkt dazu lässt sich wieder bei MONTELIUS finden, der einen geschlossenen Fund folgendermaßen definiert:

"Ein Fund in dieser Meinung - d.h. ein für chronologische Untersuchungen verwendbarer Fund oder, wie wir der Kürze wegen im Folgenden sagen, ein 'sicherer Fund' (oder nur ein Fund!) - kann als die Summe von denjenigen Gegenständen bezeichnet werden, welche unter solchen Verhältnissen gefunden worden sind, dass sie als ganz gleichzeitig niedergelegt betrachtet werden müssen".

Ferner: "Ein solcher Fund ist aber gar kein Beweis, dass sämtliche Gegenstände zur selben Zeit verfertigt wurden. Ein Gegenstand kann sehr alt, ein anderer ganz neu sein, als sie in die Erde kamen."

Im Folgenden unterstreicht er, dass je öfter zwei Typen zusammen gefunden werden, die Wahrscheinlichkeit, dass sie wirklich gleichzeitig hergestellt wurden, immer größer wird. D. h. mit anderen Worten: Jeder Gegenstand verändert sich im Laufe der Zeit mehr oder weniger schnell, auf Grund von Moden oder technologischen Neuerungen.

Mit Hilfe der kombinatorischen Methode allein lassen sich die Funde und auch die in ihnen enthaltenen Typen in eine zeitliche Reihenfolge bringen, wobei jedoch die Abfolge nicht von evolutiven Merkmalen - die man erkennen kann oder nicht - abhängig ist.

Der Ausgangspunkt der Untersuchung der Typenkombination ist der geschlossene Fund und die zeitliche Veränderung von Objekten, sei es durch technologische Verbesserungen oder sich ändernde Moden. Diese Tatsachen müssen bei der Erstellung einer Typologie ins Kalkül gezogen werden.

Im Werdegang der kombinatorischen Methode lassen sich nun verschiedene Phasen unterscheiden:

Die klassische Methode:

Nach der Erstellung einer Typologie vergleicht der Archäologe eine Anzahl von Funden und versucht, sie in Hinblick auf ihre zeitliche Entwicklung zu klassifizieren. Er bestimmt Gruppen von Funden mit verwandtem Inventar und grenzt diese zeitgleichen Funde von anderen ab. Diese Methode, die "kriminalistische" Fähigkeiten verlangt, soll durch ein kleines Beispiel, das nur aus 4 Funden und 4 Typen besteht, demonstriert werden:

Diese vier Funde (Zahlen 1-4) mögen folgende Typen (Buchstaben A-D) enthalten:

Liste 1

· Fund 1 mit den Typen C, D

· Fund 2 mit den Typen A, B

· Fund 3 mit den Typen B, C

· Fund 4 mit dem Typ D

Andererseits könnte man auch sagen:

Liste 2

· Typ A ist in Fund 2

· Typ B ist in den Funden 2, 3

· Typ C ist in den Funden 1, 3

· Typ D ist in den Funden 1, 4 enthalten

Im Allgemeinen - abgesehen von Sonderfällen - gibt es zwei Möglichkeiten:

· alle 4 Funde sind gleichzeitig,

· sie sind chronologisch verschieden.

Indem wir uns nun auf den zweiten Fall beziehen, können folgende Schlussfolgerungen gezogen werden:

Die Funde 2 und 4 haben keinen Typ gemeinsam, deshalb sollten sie zeitlich weit voneinander entfernt sein. Dasselbe kann auch für die Funde 1 und 2 gesagt werden, sie müssen ebenfalls in großem zeitlichem Abstand angesetzt werden. Das gleiche gilt auch für die Funde 3 und 4. Die Funde 1 und 3 enthalten beide den Typ C - deshalb sind sie durch diesen Typ chronologisch miteinander verbunden - sie folgen aufeinander. Das gilt auch für Fund 2 und 3 - ihre Verbindung ist durch den Typ B gegeben. Fund 1 und 4 sind über den Typ D verknüpft.

Nun möchten wir den Versuch machen, bei der Bewertung von geschlossenen Funden eine Verbindung zwischen dieser klassischen Methode und der Seriation herzustellen.

Grafische Darstellung:

Wir können die oben formulierten Beziehungen grafisch darstellen:

2...........4

2.......1

....3.......4

....3...1

2...3

........1...4

Die Abfolge der Funde muss also 2,3,1,4 lauten oder genau umgekehrt 4,1,3,2. Nur diese beiden Ordnungen können alle die oben angeführten Beziehungen erfüllen.

In gleicher Weise kann aus Liste 2 geschlossen werden, dass die Abfolge der Typen entweder A, B, C, D oder umgekehrt D, C, B, A ist. Aus den obigen Daten ergibt sich jedoch eines nicht, nämlich, welche der beiden Reihenfolgen nun die richtige ist. Um zu entscheiden, welche einer historischen Abfolge entspricht, ist es notwendig, z.B. mit Hilfe von stratigraphischen Daten oder durch eventuell vorhandene typologische Rudimente weitere Informationen zu erhalten.

Wenn wir diese Abfolge der Funde und Typen grafisch auftragen, erhalten wir ein rechteckiges, numerisches Zahlenschema (im folgenden Matrix genannt), in dem die Funde in horizontalen Reihen und die Typen in vertikalen Spalten angeordnet sind. Die Überschneidungspunkte, also die Positionen, an denen ein Fund und ein Typ zusammenfallen, zeigen eine Verteilung entlang der Hauptdiagonale, die in der Matrix von links oben nach rechts unten verläuft.

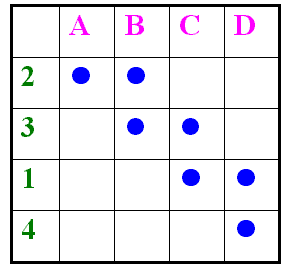Abb.1

Es war relativ einfach, die zeitliche Abfolge dieser wenigen Funde und Typen durch Überlegung zu finden. Dennoch war ein beachtlicher Aufwand an Schreibarbeit notwendig, um diese Abfolge zu beweisen. Es ist deshalb kein Wunder, dass die Argumentation für eine Chronologie eines wesentlich größeren Materials sich oft über viele Seiten hinzieht und deshalb vom Leser nur unter großem persönlichen, zeitlichen Einsatz verstanden werden kann. Außerdem ist es möglich, dass wegen der großen Anzahl der Bedingungen, die alle gleichzeitig beachtet werden müssten, dem Ersteller der Chronologie manche Bedingungen entgangen sind oder, dass er zumindest eine persönliche Auswahl an anscheinend relevanten Kombinationen getroffen hat. Deshalb wird der Leser diese Beweisführung nicht mehr leicht nachvollziehen können.

Ein viel leichter überprüfbarer Zugang zur Chronologie besteht jedoch darin, die Prinzipien der Chronologie einmal durchschaubar zu formulieren und z. B. diese Matrix - wie oben beschrieben - durch einen rein mechanischen Prozess zu erhalten, wie wir gleich besprechen werden.

Mechanische Methoden:

Streifenmethode von Sir William Mathew FLINDERS-PETRIE:

Foto von Flinders-Petrie

Zwischen 1884 und 1899 deckten FLINDERS-PETRIE und QUIBELL vier größere prädynastische Gräberfelder in Ägypten Naqada (im Süden), Hu, Abadiyeh und Ballas(im Norden), auf.

Zusammen ergaben sich an die 3900 Grabfunde mit zahlreichen keramischen Beigaben. PETRIE erkannte, dass es möglich war, lediglich unter Benutzung der Information der darin enthaltenen Artefakte, eine zeitliche Ordnung der einzelnen Gräber zu erhalten. Er wählte 900 Gräber für seine Analyse aus.

Zur Erstellung seiner Typologie unterschied er lediglich neun verschiedene Keramikklassen, für jede von ihnen erstellte er eine typologische Reihe. Diese Reihen überprüfte er mittels der Kombinationen auf ihre Parallelität. So erhielt er an die 600 Typen. Insofern nahm er bereits die typologische Methode MONTELIUS vorweg. Er ging aber noch weiter, indem er nun die Sequenz der Gräber feststellen wollte.

Dabei ging er folgendermaßen vor: Jedes einzelne Grab wurde in Form eines Pappkartonstreifens (ungefähr 18 cm x 1 cm) kodiert. Für jede Keramikklasse war eine Spalte vorgesehen, in die dann die Nummer des entsprechenden Typs eingetragen wurde.

Diese 900 Streifen wurden nun Breitseite an Breitseite in einer Reihe untereinander gelegt und solange umgeordnet, bis die gleichen Zahlen in den entsprechenden Spalten der Streifen möglichst beisammen lagen. Die Länge der ganzen Reihe betrug etwa 9 m. Man kann sich vorstellen, welcher Zeitaufwand hinter diesem gewaltigen Sortierprozess stand.

Nach diesem Ordnungsvorgang teilte er die 900 Gräberstreifen in 51 gleich große Gruppen, nummeriert von 30 bis 80, um später gefundene sowohl ältere Gräber von 1-30 als auch jüngere nach dieser Sequenz von 80-100 einordnen zu können. Diese Gruppen sind seine Sequenzdaten (SD), die wir auch für unsere Arbeit - allerdings mit den Werten von 1-1000 - verwenden wollen. Leider liegen Petrie‘s ursprüngliche Daten heute nicht mehr vor und somit können seine Resultate mit modernen Methoden nicht überprüft werden. Inhaltlich fanden sie jedoch eine Bestätigung bei der Bearbeitung anderer Gräberfelder.

Chronologische Stufen und deren keramische Leitformen Abb. 1 aus Flinders Petrie (1899).

Bei seiner Methode veränderte PETRIE die starre, von Anfang an vorgegebene Anordnung der Typen nicht, was jedoch ebenfalls erwünscht sein kann, wie im Folgenden demonstriert werden soll.

Streifenmethode mit Zeilen- und Spaltenvertauschung:

Zur Demonstration der Vorgangsweise kehren wir zu unserem Beispiel zurück.

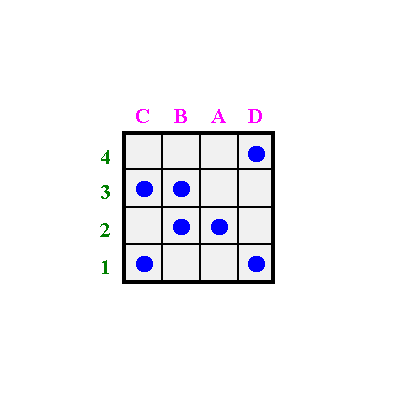
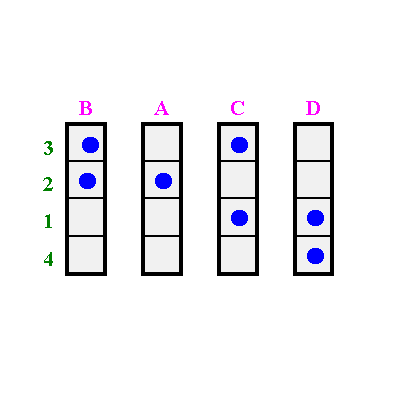
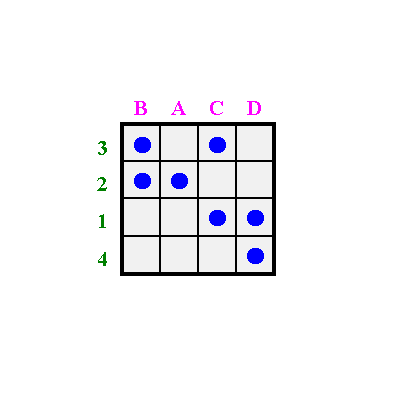
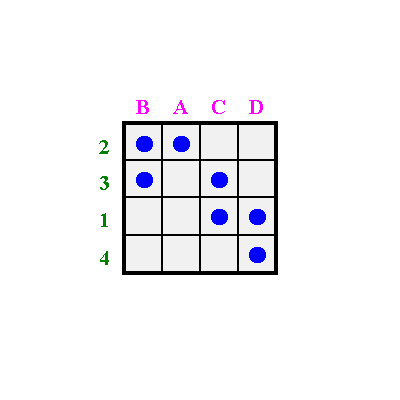
Zu Beginn wird die zufällig angeordnete 4x4 Matrix (oben) in horizontale Reihenstreifen zerschnitten (unten)

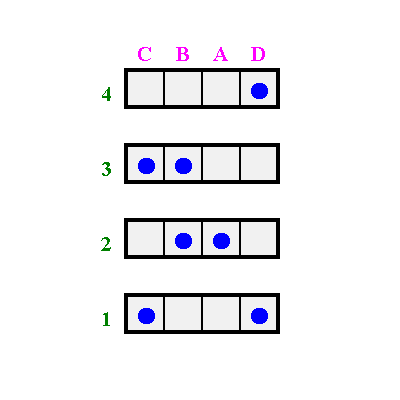
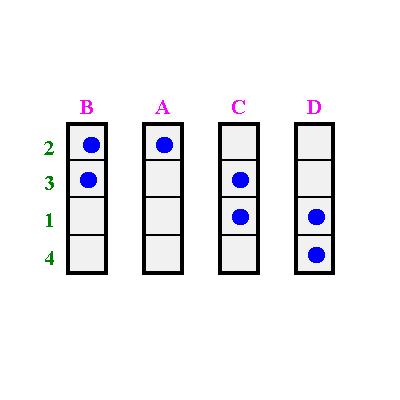
Diese Reihen werden solange vertauscht, bis die Punkte so nahe wie möglich an die Diagonale herangeführt werden.

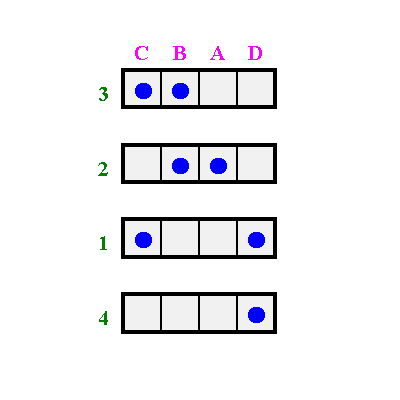
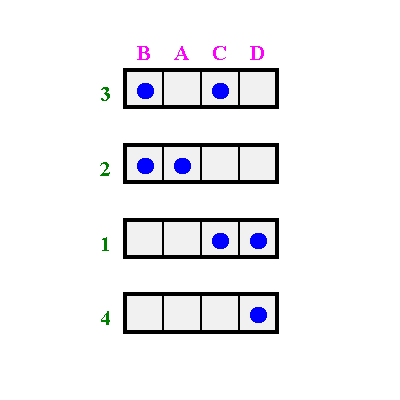
Jetzt wird diese Matrix ein zweites Mal aufgezeichnet.

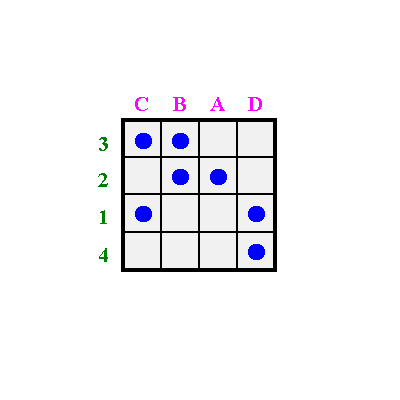
Sie wird nun senkrecht in Spaltenstreifen zerschnitten.

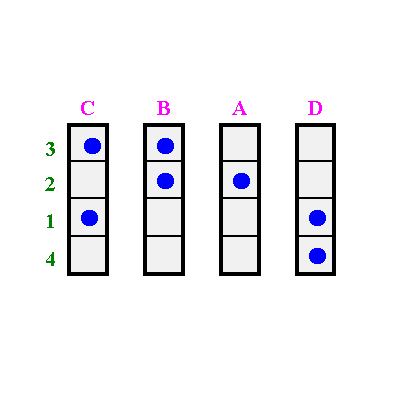
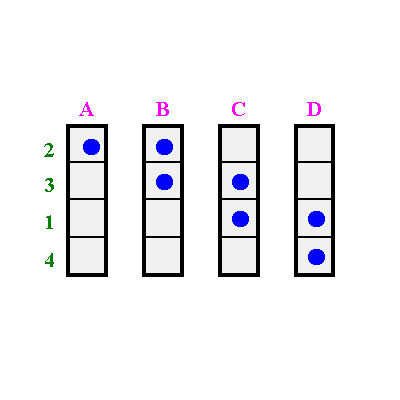
Die Spalten werden ebenfalls solange miteinander vertauscht werden, bis sich die Punkte in der Nähe der Diagonale konzentrieren.

Dann beginnt man wieder von vorne, zeichnet von neuem und zerschneidet wieder in Reihenstreifen usw.

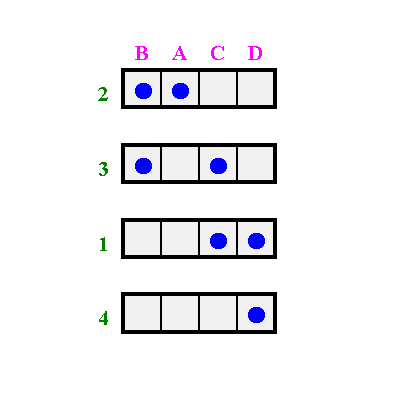
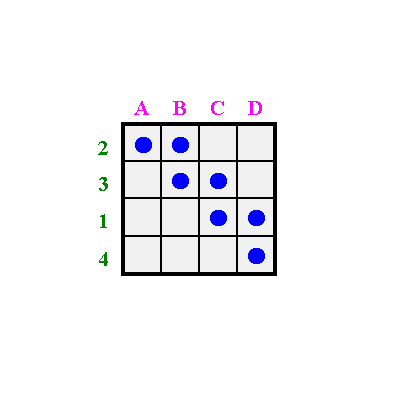
Dieser Prozess wird nur solange durchgeführt, bis eine weitere Vertauschung der Reihen oder Spalten keine Verbesserung des Resultats erbringen kann

Im Folgenden gibt es dazu eine Animation: Dabei werden die Einzelbilder in einem speziellen Format (Animated GIF) abgespeichert und schnell hintereinander wiedergegeben.

Man kann sich sehr leicht vorstellen, dass schon bei Matrizes mit ca. 20 Funden mal 20 Typen ziemlich viele Arbeitsschritte zur Erreichung des gewünschten Resultates notwendig werden.

Dieses Phänomen der Anordnung der Besetzungspunkte an der Diagonale wird nach ihrem Entdecker FLINDERS-PETRIE "PETRIE'SCHES Konzentrationsprinzip" oder "Petrifikation" genannt.

Mathematische Verfahren und entsprechende Algorithmen für Computerprogramme:

Der AXIS-Algorithmus:

Aus einer großen Anzahl von Vorschlägen, wie man die Seriation mit mathematischen Mitteln durchführen könnte, wollen wir uns zunächst mit demjenigen beschäftigen, der uns der elementarste Ansatz zu sein scheint. Unabhängig voneinander kamen die drei Wissenschaftler WILKINSON, LEGOUX und GOLDMANN zur selben Lösung. Ihre arithmetische Vorschrift - im Folgenden werden wir eine solche Vorschrift Algorithmus nennen - sieht folgendermaßen aus:

1. Berechne die Mittelwerte der Besetzungen (Inzidenzen) in den Spalten.

2. Ordne die Spalten in Abhängigkeit von ihren Mittelwerten.

3. Berechne die Mittelwerte der Besetzungen in den Reihen.

4. Ordne die Reihen entsprechend ihren Mittelwerten.

5. Beginne von vorne und setze solange fort, wie es notwendig ist.

Um diese - für Mathematiker trivialen, aber für viele Archäologen vielleicht immer noch "zu mathematischen "- Formulierungen zu erklären, möchten wir eine Anwendung mit unserem Beispiel, jedoch mit einer anderen Ausgangsordnung zeigen.

Abb. 3/1

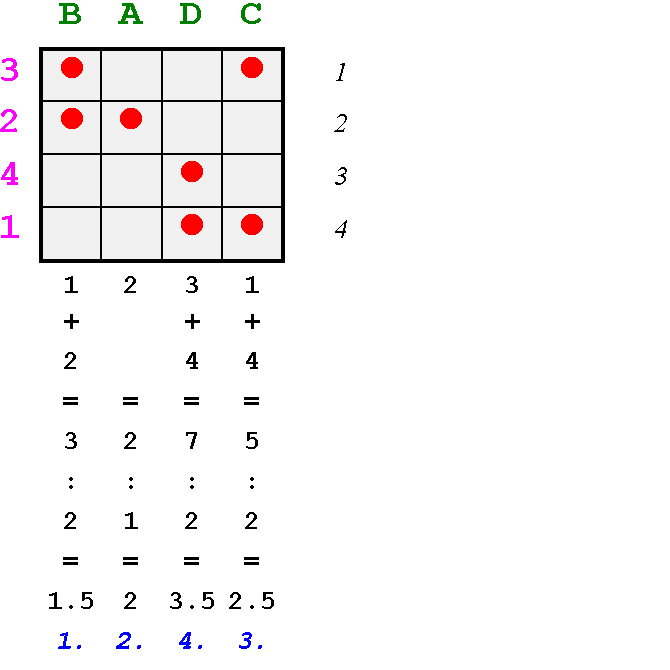
Zuerst suchen wir die Inzidenzpunkte des Typs B in den Funden 3 und 2 und notieren uns ihre Position, die durch die rechts außerhalb stehende Ordnungszahl der zugehörigen Zeilen angezeigt ist. Der Fund 3 enthält einen Inzidenzpunkt mit dem Typ B in der Position 1. Diesen Einser schreiben wir unter die Spalte von B. Die 2. Besetzung wird im Fund 2 an der Position 2 gefunden, wir schreiben unter obig notierten Einser einen Zweier. Unter der Spalte B stehen nun die Zahlen 1 und 2, sie werden addiert und durch die Anzahl der Besetzungen dividiert - in diesem Fall durch 2. Das Resultat (1,5) ist der Mittelwert der Inzidenzpunkte in der Spalte B. Wir gehen ganz analog mit den Spalten A, D und C vor - so erhalten wir die Mittelwerte aller Spalten. Bis jetzt haben wir nur den Punkt (1) des Algorithmus der Seriation erfüllt.

Für den Punkt (2) ordnen wir nun die Spalten entsprechend ihren Mittelwerten um: die Spalte B mit dem niedrigsten Mittelwert von 1,5 kommt an die erste Stelle, gefolgt von A mit dem Mittelwert 2, von C mit 2,5 und zuletzt D mit 3,5. So erhalten wir die neugeordnete Matrix.

Abb. 3/2

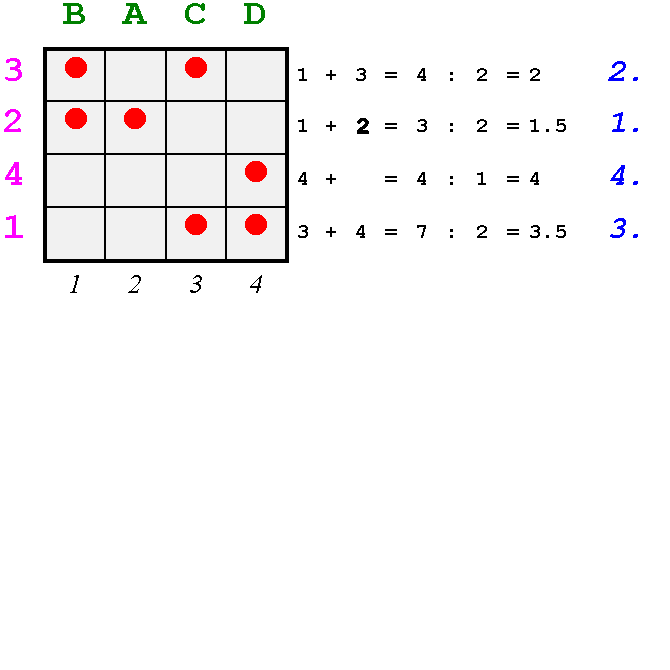
Punkt (3) der arithmetischen Vorschriften verlangt die Berechnung der Mittelwerte der Reihen dieser neuen Matrix, die Zwischenergebnisse sind an der rechten Seite der Matrix (Abb. 3/2) niedergeschrieben. Die erforderlichen Positionsnummern sind unterhalb der Matrix zu finden. Für Punkt (4) werden diese Reihen so umgeordnet, dass die Reihe mit dem niedrigsten Mittelwert zuoberst liegt usw.

Nun beginnt die gesamte Prozedur von vorne.

Abb.3/3

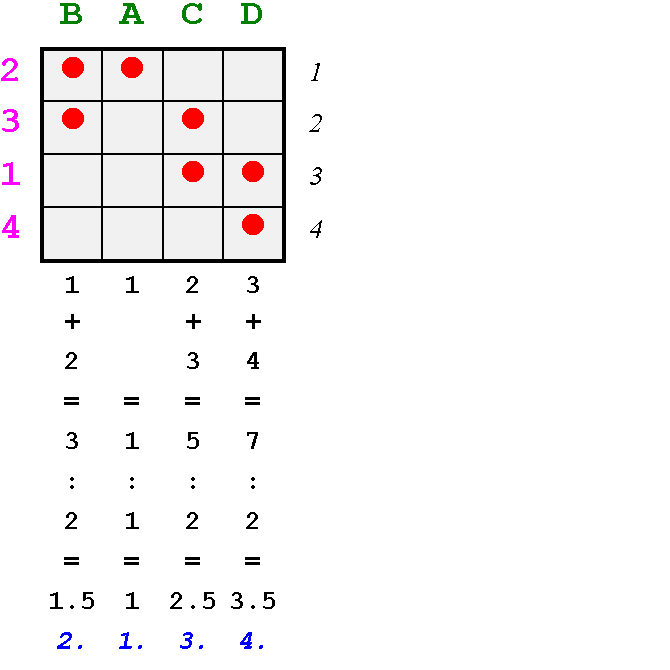
Der Abbruch erfolgt nach zweimaliger Durchführung der Schritte (1) - (5). Man kann nun aus Abb. 3/4 ersehen, dass die Reihen aufsteigende Mittelwerte besitzen. Eine Fortsetzung wäre also unnötig und ergäbe keine weitere Veränderung der Matrix. So haben wir also mit Hilfe dieses mathematischen Verfahrens dasselbe Resultat wie mit der klassischen und auch mit der Streifenschneidemethode erreicht. Anwendungsbeispiele, bei denen eine viel größere Zahl von Funden und Typen vorliegt, werden bald zu sehr langwierigen Berechnungen führen und nur ein Computer kann hier weiterhelfen. Genauso wie wir die Erklärung der Prinzipien der mathematischen Vorschrift in kleine, verständliche Schritte zerlegt haben, wird dies in einem Computerprogramm getan, damit der Computer diese Vorschrift "verstehen" kann.

Abb.3/4

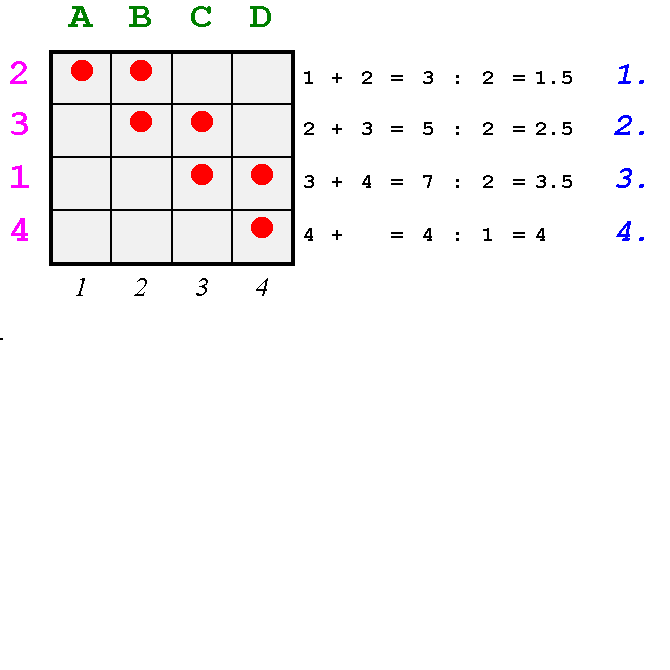
Hier die Animation des Rechenvorganges:

Das Axiom der Seriation:

Diejenige Ordnung einer Inzidenzmatrix von archäologischem, chronologisch auswertbarem Material, die eine optimale Anordnung aller Inzidenzpunkte entlang der Hauptdiagonalen ergibt, zeigt die durchschnittliche zeitliche Abfolge der Typen und Funde. Die Richtung dieser Abfolge muss mit anderen Mitteln bestimmt werden.

Korrespondenzanalyse oder Reciprocal Averaging:

Von kleinen Unterschieden abgesehen, ist der AXIS-Seriationsalgorithmus mit der in der Mathematik seit etwa 1970 in Mode gekommenen Korrespondenzanalyse ident. Bei diesem Verfahren sollen Zeilen und Spalten einer Kontingenztafel (=Matrix) so geordnet werden, dass die Korrelation zwischen ihnen ein Maximum wird.

Diese Kontingenztafel ist genauso wie die Inzidenzmatrix ein rechteckiges Zahlenschema. Nur sind hier die Inzidenzen zwischen einer Zeile und Spalte nicht durch 0 oder 1 ausgedrückt, sondern durch die absoluten Häufigkeiten. Wäre z. B. ein Typ in einem Fund dreimal enthalten, so würde in die Kontingenztafel an der Überschneidungsstelle 3 einzutragen sein. Anstelle der Rangordnungen wird hierbei direkt mit den Mittelwerten operiert. Der Vorteil dieses Algorithmus liegt darin, dass das zeitaufwendige Sortieren der Schwerpunkte entfallen kann. Außerdem ist dieses Verfahren auch besser mathematisch fundiert.

Der von IHM vorgeschlagene Algorithmus zur Durchführung einer Seriation sieht nun folgendermaßen aus:

· (1) Belegen der Schwerpunkte der Zeilen mit ihrer Ordnungszahl.

· (2) Belegen der Schwerpunkte der Spalten mit ihrer Ordnungszahl.

· (3) Berechnung der Schwerpunkte der Zeilen aus den absoluten Häufigkeiten der Besetzungen unter Verwendung der bisherigen Mittelwerte (anstelle der Rangordnungen) für die Spalten.

· (4) Standarisierung der für die Zeilen erhaltenen Schwerpunkte.

· (5) Besetzung der Mittelwerte der Spalten mit ihren absoluten Häufigkeiten der Besetzungen unter Verwendung des bisherigen Mittelwertes für die Zeilen.

· (6) Standarisierung der Schwerpunkte für die Spalten.

· (7) Abbruch, wenn die letzte Veränderung für jeden Schwerpunkt der Zeilen unter einem vorgegebenen Wert Epsilon liegt.

· (8) Abbruch, wenn die letzte Veränderung für jeden Schwerpunkt der Spalten unter einem vorgegebenen Wert Epsilon liegt.

· (9) Neubeginn bei (3).

Die Schritte (1) und (2) werden nur beim 1. Durchlauf vollzogen, um die Schwerpunktsvektoren zu initialisieren. Die Standarisierungen in den Schritten (4) und (6) sind notwendig, damit die Mittelwerte nicht zu stark expandieren.

Unter Standardisierung oder z-Transformation versteht man in der mathematischen Statistik eine Transformation einer Zufallsvariablen, so dass die resultierende Zufallsvariable den Erwartungswert Null (=Zentrierung) und die Varianz (Standardabweichung) Eins (=Normierung) besitzt. Die Standardabweichung entspricht der Wurzel der Varianz und ist somit auch gleich Eins.

Zum Abschluss dieses Abschnittes sei eine Animation des Verlaufes der Seriation beim Reciprocal Averaging anhand des awarischen Fundmaterials dargestellt.

Prinzip der Dynamischen Typologie:

Für jede Seriation ist die Typologie ausschlaggebend. Da die Typologie oft sehr subjektiv ist, versucht man nun aus einer starren statischen Typologie zu einer objektiv besseren dynamischen Typologie zu gelangen.

Unser Konzept für die dynamischen Typologie bedeutet folgendes: Wenn ein Typ in einem Seriationsergebnis als Durchläufer erscheint, kann das mehrere Ursachen haben, unter anderem könnten hier Typen vermengt oder zu grob gefasst worden sein. Wenn sich Merkmale eines Typs in einem älteren Abschnitt signifikant von Merkmalen im jüngeren Bereich unterscheiden, so können durch Aufspaltung zwei neue Typen erhalten werden. Insgesamt führt dieses Verfahren zu einer Seriationsverbesserung.

Dynamische Typologie ist somit nichts anderes als eine lernfähige Typologie. Die Typologie wird von Zwischenergebnissen beeinflusst und verändert. Diese Veränderung wirkt sich natürlich wieder auf das Seriationsresultat aus. In einem iterativen Prozess gelangt man somit in mehreren Schritten zu einer Typologie, die optimal an die Forderungen, chronologische Merkmale zu entdecken, angepasst ist.

Die Seriation bewährt sich vor allem dort, wo keine anderen Methoden wirksam werden können. Sie liefert eine mittlere Abfolge der verschiedenen Merkmale/Typen und Fundkomplexe.

Das Prinzip der dynamischen Typologie soll anhand eines einfachen Beispiels dokumentiert werden.

Abbildung Dynamische Typologie  I.

1

2

3

4

5

6

7

8

9

10

11

A

●

●

A

B

●

●

●

●

B

C

●

●

●

●

C

D

●

●

●

●

D

E

●

●

●

E

F

●

●

●

F

G

●

●

●

G

H

●

●

●

●

H

I

●

●

●

●

I

J

●

●

●

J

1

2

3

4

5

6

7

8

9

10

11

Wie sehen, dass der Typ 6 offensichtlich ein Durchläufer ist. Er kann nun wirklich ein Durchläufer sein, wenn wir in keinem Merkmal Hinweise auf eine zeitliche Dynamik feststellen können. Es könnte aber auch anders sein, wie wir im Folgenden sehen werden. 

Abbildung Dynamische Typologie  II.

1

2

3

4

5

6

7

8

9

10

11

A

●

●

A

B

●

●

●

●

B

C

●

●

●

●

C

D

●

●

●

●

D

E

●

●

●

E

F

●

●

●

F

G

●

●

●

G

H

●

●

●

●

H

I

●

●

●

●

I

J

●

●

●

J

1

2

3

4

5

6

7

8

9

10

11

Stellen wir uns nun vor, dass sich im Typ 6 die oberen vier Besetzungspunkte durch ein signifikantes Merkmal von den unteren vier Vertretern unterscheiden. Dies markieren wir zunächst durch die unterschiedlichen Farben rot und grün.

Nun ist es gerechtfertigt, den ursprünglichen Typ 6 in die zwei Typen 6a und 6b aufzuspalten. Das Ergebnis sehen wir in Textabbildung 22: Typ 6a ist nun viel früher zu finden, Typ 6b viel später als vorher Typ 6, insgesamt ist es zu einer Verbesserung des Seriationsergebnisses gekommen, denn es gibt keine Durchläufer mehr.

Abbildung Dynamische Typologie III.

1

2

3

6a

4

5

7

6b

8

9

10

11

A

●

●

A

B

●

●

●

●

B

C

●

●

●

●

C

D

●

●

●

●

D

E

●

●

●

E

F

●

●

●

F

G

●

●

●

G

H

●

●

●

●

H

I

●

●

●

●

I

J

●

●

●

J

1

2

3

6a

4

5

7

6b

8

9

10

11

Falko Daim meint in DAIM Falko 1987, Das awarische Gräberfeld von Leobersdorf, NÖ. Studien zur Archäologie der Awaren  003, Seite 28, „Definitionen von Typen können – beachtet man die Grundregeln – nicht richtig oder falsch, sondern nur vom pragmatischen Gesichtspunkt her günstig oder ungünstig sein.“

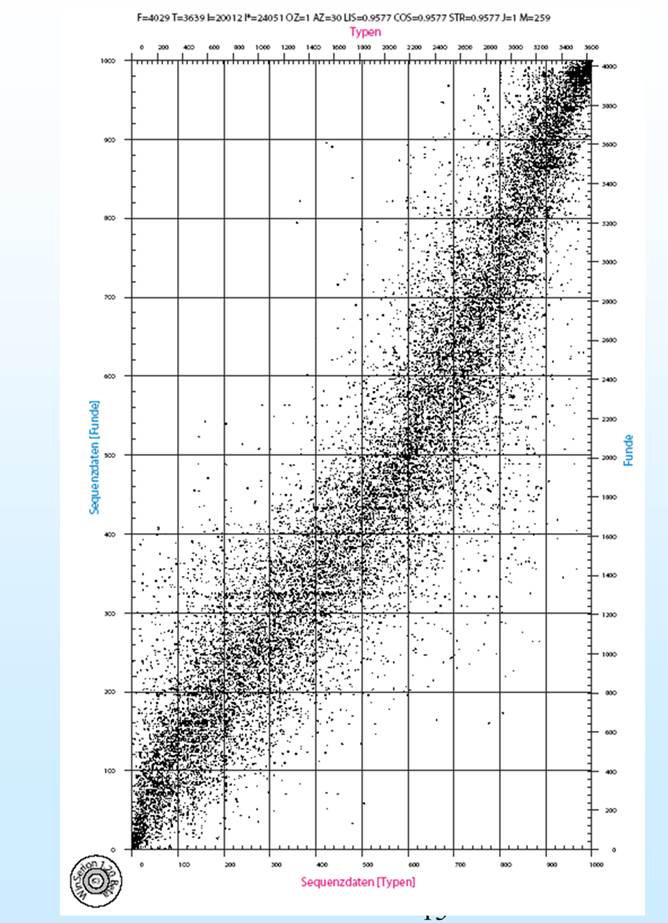
Seriation awarenzeitlicher Männergräber.

Jeder Punkt entspricht einem Gegenstand. In den Spalten sind die mehr als 3600 Typen angeordnet, in den Reihen die mehr als 4000 Fundkomplexe.

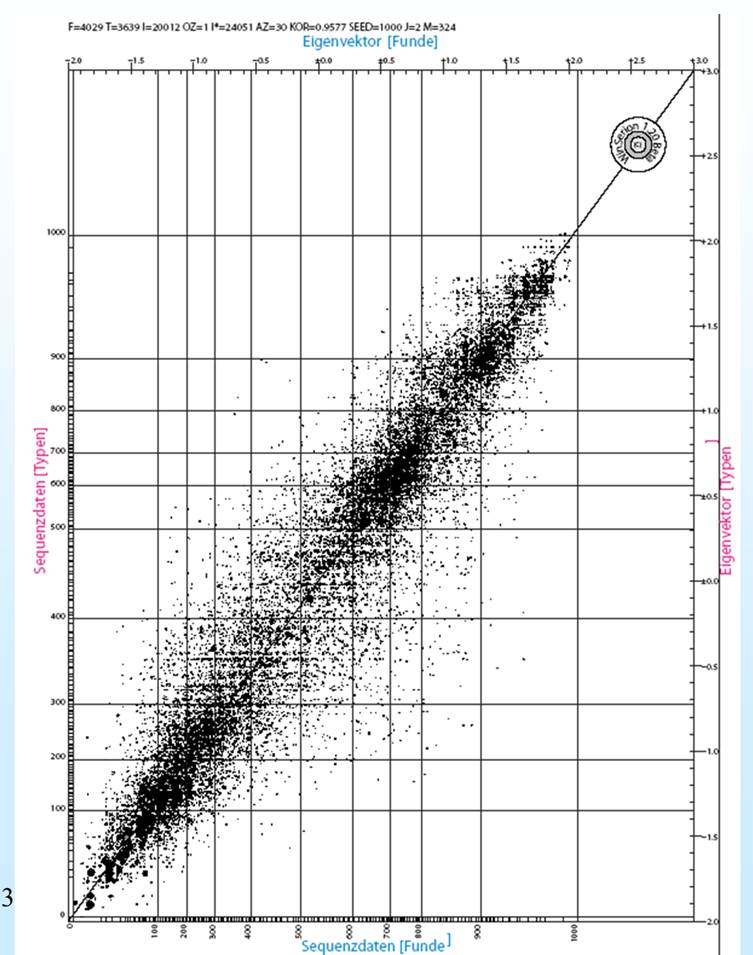
Seriation awarenzeitlicher Männergräber. Darstellung in Eigenvektorform.

Dadurch liegen Fundkomplexe mit den gleichen Typen nicht wie bei voriger Abbildung nebeneinander sondern übereinander. Dadurch kommt es stellenweise zu stärkeren Anhäufungen.

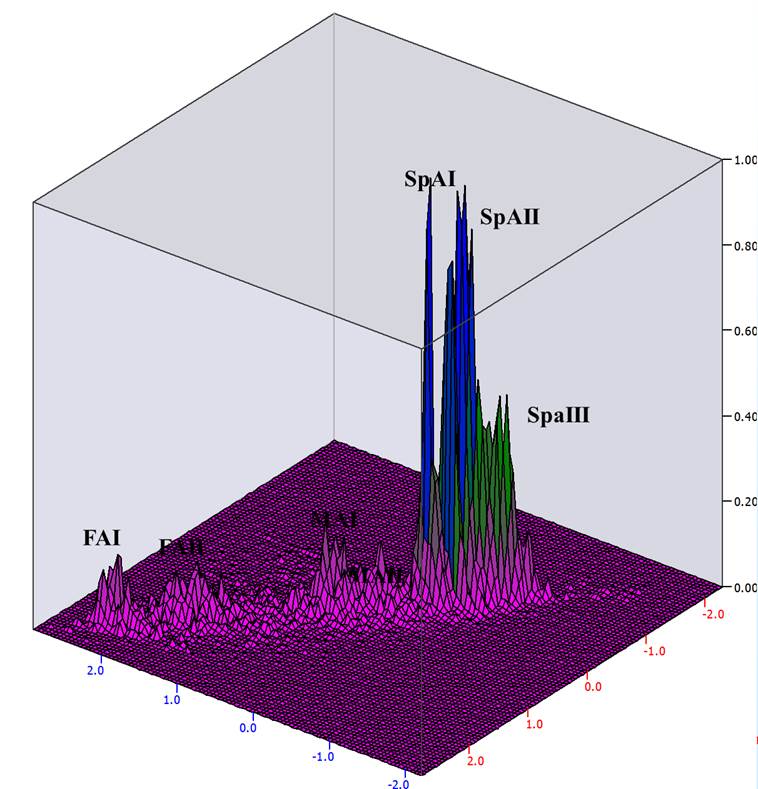
Darstellung der Eigenvektoren des Seriationsergebnisses der awarenzeitlichen Männergräber in 3D.

Die erhaltenen Gipfel wurden mit den gegebenen chronologischen Stufen benannt.

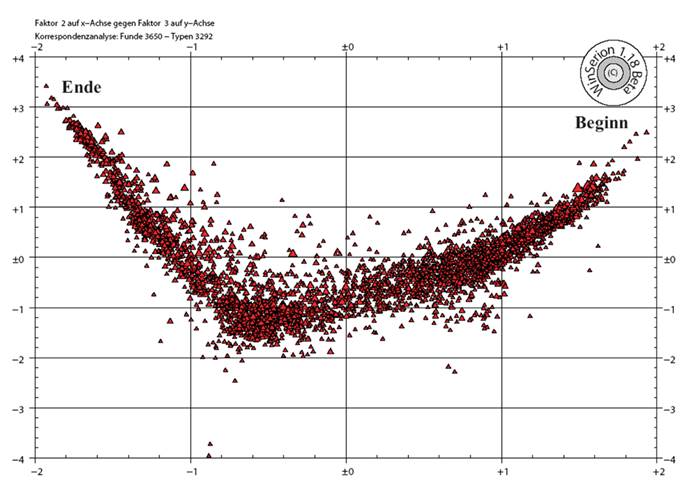
Awarische Männergräber, Korrespondenzanalyse mit dem gesamten Datensatz, Komplexe. Jedes Dreieck entspricht einem Fundkomplex.

Je größer ein Dreieck ist, desto mehr datierendes Fundmaterial ist in dem Fundkomplex enthalten. Die Anordnung in Form einer Parabel zeigt den zeitlichen Verlauf, der Anfang ist markiert durch „Beginn“, das Ende durch „Ende“. Rechts oben knapp nach dem Beginn sieht man benachbart zwei besonders große Dreiecke. Es handelt sich um das „Kaganengrab“ von Kunbábony und das „Fürstengrab“ von Bócsa. Entgegen geläufigen Vorstellungen datieren diese beiden Komplexe an den Beginn der Awarenzeit, wahrscheinlich noch vor 600 n. Chr.

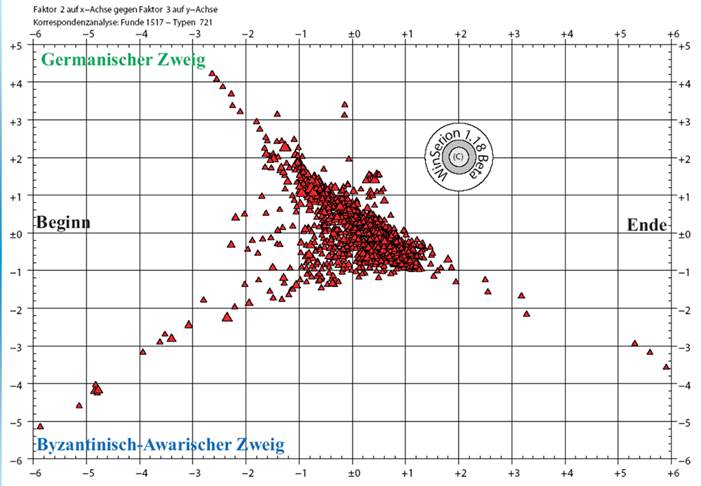
Seriation Awarische Frauengräber, Korrespondenzanalyse mit dem gesamten Datensatz, Komplexe.

Hierbei wird nicht nur eine Parabel erhalten sondern sogar zwei. Vor allem in der Frühawarenzeit, links in der Grafik, ist das Fundmaterial in den beiden Zweigen sehr unterschiedlich. Der obere Zweig enthält eigentlich merowingerzeitliche Schmuckgegenstände, der untere Zweig dagegen hauptsächlich Frauenschmuck byzantinischer Provenienz. Der obere Zweig kann also als von Germaninnen im Awarenreich interpretiert werden, der untere von Awarinnen und Slawinnen. Der Zweig beider Parabeln ganz rechts zeigt Charakteristika slawischer Frauengräber des 9. Jh.s.

letzte Bearbeitung 2.12.2019